篇1:12.1 函数 第2课时 课件(共16张PPT) 沪科版八年级数学上册点此进入下载文字摘要:(共16张PPT)第十二章 一次函数12.1 函数12.1.2 函数的三种表示方法1.知道表示函数有三种方法,会用列表法、解析法表示函数关系;2. 掌握函数自变量范围的确定和函数值的求法;3.能根据实际问题的已知条件,列出简单的函数关系的表达式.任务一:了解并掌握函数的三种表示方法. 活动:回想上一节课研究的三个问题.问题1:用热气球探测高空气象.{10A1B5D5-9B99-4C35-A422-299274C87663}时间t/min01234567…海拔高度h/m18001830186018901920195019802010…问...(全国地区适应) 图片预览:  篇2:3.2分式的约分 课件(19张ppt) 青岛版数学八年级上册点此进入下载文字摘要:3.2 分式的约分 1.了解分式约分的意义,理解最简分式的概念. 2.掌握分式约分的方法和步骤,能熟练进行计算. 学习目标 分式的基本性质 分式的分子与分母都乘(或除以)同一个不为0的整式,分式的值不变. 式子表示 知识回顾 AB=A·MB·M ,AB=A÷MB÷M (M≠0), 其中A,B,M是整式. ? 将下列式子因式分解 (1)10x2?5x= ? (2)4a2?b2= ? (3)m2?6m+9= ? 5x(2x?1) ? (m?3)2 ? (2a+b)(2a?b) ? 课堂导入 你还记得如何化简分数1216吗? ? 分数的约分...(青岛市地区适应) 图片预览:   篇3:浙教版数学八年级上册 1.6尺规作图 课件(共25张PPT)点此进入下载文字摘要:(共25张PPT)第一章 三角形的初步认识1.6 尺规作图学习目标1.了解尺规作图,掌握尺规作图的步骤:画一个角等于已知角,画已知线段的垂直平分线.2.掌握三角形的基本作图方法,能熟练使用尺规进行三角形的实际作图.3.掌握尺规作图的简单应用,能解尺规作图题.问题引入请画出和一个与∠1相等的角.12∠1= ∠2如果限定只能用圆规和没有刻度的直尺, 你还能画出来吗?探究新知如何用尺规作图得到一些基础几何图形呢?尺规作图:在几何作图中,我们把用圆规和没有刻度的直尺作图简称为尺规作图.探究一作一个角等于已知角已知: ∠AOB.求作: ∠A′O′B′,使∠A...(全国地区适应) 图片预览:   篇4:2.1 认识无理数 课件 北师大版八年级上册数学 课件(17张PPT)点此进入下载文字摘要:(共17张PPT)第二章 实数012.1 认识无理数1.了解无理数的基本概念,感受无理数产生的实际背景和引入的必要性;一、学习目标2.知道有理数和无理数的区别,并能够判断一个数是有理数还是无理数;3.能借助计算机估算一个无理数的范围.二、新课导入有以下两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大的正方形.11三、概念剖析(1)设大正放形的边长为a,a满足什么条件?a由勾股定理可知,两直角边的平方和等于斜边的平方,所以a满足条件:12+12=a2, 即a2=2.(2)a可能是整数吗?(3)a可能是分数吗?不可能不可能事实上,我们可以证明,在等式a...(全国地区适应) 图片预览:  篇5:初中数学人教版八年级下册17.1《勾股定理》课件 20张PPT点此进入下载文字摘要:(共20张PPT)探索勾股定理abc相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用正方形瓷砖铺成的地面中反映了直角三角形三边的某种数量关系。我们也观察下图中地面,看看能发现什么?情景引入等腰直角三形等腰直角三角形三边有怎样的数量关系呢 两边之和大于第三边,两边之差小于第三边.等腰直角三形等腰直角三角形三边还有其他的数量关系吗 如图上图是截取瓷砖的一部分, 观察两小正方形面积与大正方形面积有什么数量关系 请同学们思考,并说说你怎样得到的.探究活动一:ACBABCA的面积与B的面积和=C的面积即:SA+SC=SCCBACBA...(全国地区适应) 图片预览: 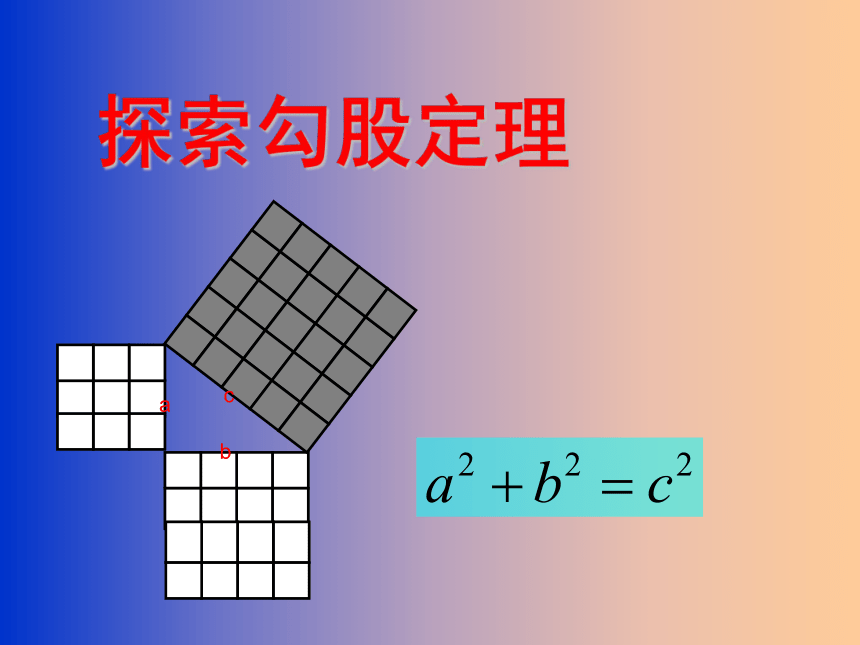 篇6:2.4 估算 课件(19张PPT) 北师大版八年级上册数学点此进入下载文字摘要:(共19张PPT)第二章 实数2.4 估算1.能通过估算检验计算结果的合理性.一、学习目标2.能估计一个无理数的大致范围,并能通过估算比较两个数的大小.3.能够运用估算解决生活中的实际问题.二、新课导入有一位叫希帕索斯的学生提出了一个问题:‘边长为1的正方形,其对角线的长是多少呢?’ 运用勾股定理计算是 ,发现 既不是整数也不是整数的比 . 的出现让人们认识到了无理数,但 的值为多少呢?三、概念剖析某地开辟了一块长方形的荒地,新建一个环保主题公园.已知这块荒地的长是宽的两倍,它的面积为400000m2.(1)公园的宽...(全国地区适应) 图片预览:   篇7:4.2立方根 课件(共28张PPT)八年级数学上册苏科版点此进入下载文字摘要:(共28张PPT)第4章 · 平方根4.2 立方根学习目标1. 了解立方根的概念,会用根号表示数的立方根;2. 了解开立方与立方是互逆的运算,会用立方运算求一些数的立方根;3. 能运用立方根解决一些简单的实际问题.传说中,公元前429年,一场瘟疫袭击了希腊第罗斯岛(Delos),造成四分之一的人口死亡.岛民们推派一些代表去神庙请示阿波罗的旨意,神指示说:要想遏止瘟疫,得将阿波罗神殿中那正立方的祭坛加大一倍.人们便把每边增长一倍送到神那儿,于是神更加发火,他说,你们竟敢愚弄我!我要加倍惩罚你们!第罗斯岛人只好去求救于当时著名的学者柏拉图.数学小故事倍立方问题开始,柏拉图和他的...(全国地区适应) 图片预览:   篇8:4.4 近似数 课件(共19张PPT) 苏科版数学八年级上册点此进入下载文字摘要:(共19张PPT)4.4 近似数2、全球有40亿人收看了北京奥运会开幕式的电视转播。1、某班有54名同学。请问:这两个数据有什么区别?生活中有些数据是真实准确的,有些数据是近似的。准确数近似数情境引入1.下列数据中,哪些是准确数?哪些是近似数?练一练(1)某词典有1752页;(2)量杯里有水50 ml;(3)男子短跑100m世界纪录为9.58s;(4)世界人口已有61亿.2.下列数据中(画线部分),不是近似数的是( )A . 2004年雅典奥运会上,刘翔110m跨栏的成绩为12.91s;B . 世界人口已有65亿;C . 印度洋海啸,国际社会向灾区捐款捐...(全国地区适应) 图片预览:   篇9:第11章 三角形 数学活动 镶嵌 课件 人教版数学八年级上册(共23张PPT)点此进入下载文字摘要:(共23张PPT)第十一章 三角形数学活动 镶嵌学习导航学习目标新课导入概念剖析典型例题当堂检测课堂总结1.知道镶嵌的意义,会用一种或几种正多边形进行平面的镶嵌;(重点、难点)2.知道可以用一些全等的非正多边形进行平面的镶嵌;一、学习目标3.通过对可进行平面镶嵌的多边形的探究,体会数学与生活的密切联系.二、新课导入生活中的镶嵌思考:在生活中有没有遇到正五边形的瓷砖铺成的地面或墙面?为什么?三、概念剖析用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖.从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆...(全国地区适应) 图片预览:  篇10:【核心素养目标】苏科版八年级数学上册第4章 实数 复习课 课件 (共26张PPT)点此进入下载文字摘要:(共26张PPT)第4章 实数第4章 复习课1.知道平方根、算术平方根、立方根的概念,能用开平方或开立方运算求一个数的平方根或立方根.2.知道无理数和实数的概念,会对实数进行分类,能进行简单的实数四则运算.3.会求实数的绝对值、相反数,会进行实数的大小比较.进一步体会数形结合及分类思想在数学中的重要性.◎重点:会求一个非负数的平方根、算术平方根及实数的立方根,会进行实数的运算.◎难点:算术平方根的意义及实数的性质.请回顾一下,这一章我们学习了哪些知识.·导学建议·本节复习课的主体是知识的再现,可先让学生课前自主复习,回顾这一单元所学知识点,并将自己认为重要的知识点记录整理....(全国地区适应) 图片预览:  篇11:14.3.提公因式法 课件 人教版数学八年级上册(48张PPT)点此进入下载文字摘要:(共48张PPT) 提取公因式法14.3因式分解14.3.1提取公因式法202X把一个多项式化成几个整式的乘积的形式。 提取公因式法因式分解:学习新知202X把一个多项式化成几个整式的乘积的形式。 提取公因式法因式分解:2、利用整式乘法检验因式分解的正确性。和差积整式的乘法因式分解1、请你举例a2+2ab+b2=(a+b)2a2-b2=(a+b)(a-b)类比思想:实现了旧知识向新知识的拓展延伸 提取公因式法思考:整式的乘法与因式分解有什么关系吗?(×)(√)(×) 对象是乘积结果是和差用整式乘法检验知识应用?经验提升...(全国地区适应) 图片预览:   篇12:人教版数学八年级上册 13.1.1轴对称课件 23张PPT点此进入下载文字摘要:(共24张PPT)13.1.1轴对称(第1课时)《奇妙的对称美》脸谱艺术车标设计剪纸艺术要仔细观察哦!1、动一动:尝试剪出一个简单的对称图形2、说一说:怎样剪出一个对称图形?4、将上图中的每一个图形沿某条直线折叠,直线两旁的部分能完全重合吗?3、观察这些图形有什么共同的特征?如果 沿一条直线折叠,直线两旁的部分能够 _________,那么这个图形就叫做__.这条 叫做__.对称轴一个平面图形完全重合轴对称图形对称轴对称轴轴对称图形轴对称图形一、轴对称图形定义直线注意:1....(全国地区适应) 图片预览:   篇13:人教版八年级数学上册 15.3.1分式方程(一) 课件 (共17张PPT)点此进入下载文字摘要:(共17张PPT)欢迎来到数学乐园请同学们完成导案一、二两部分(尝试列方程)电影《哪吒之魔童降世》,一上映就获得全国人民的追捧,某电影院第一天售票总额约4000元,第二天售票总额约12000元,第二天比第一天多售出200张票,已知两天的票价相同,求第一天售出多少张票?列一列解:设第一天售出x张票.15.3.1分式方程(1)1.了解分式方程的概念;2.会解可化为一元一次方程的简单分式方程,从中体会类比和转化的数学思想;3.了解需要对分式方程的解进行检验的原因.目标导航分母中含有未知数的方程叫做分式方程。以前学过的分母中不含有未知数的方程叫做整式方程 。说一说下列式子中...(全国地区适应) 图片预览:  篇14:【核心素养目标】 苏科版数学八年级上册1.1 全等图形 课件(共21张PPT)点此进入下载文字摘要:(共21张PPT)第1章 全等三角形1.1 全等图形1.认识全等图形,能说出全等图形的概念和特征.2.观察有关的图案,并能识别其中的全等图形.3.通过观察、画图等活动,感受图形的变化,积累对全等图形的体验.◎重点:理解全等图形的概念和特征.◎难点:通过观察、画图等活动,感受图形的变化,积累对全等图形的体验.下列各组图形的形状与大小有什么特点?你能给这样的图形起个名字吗?·导学建议·从生活中熟悉的图片着手,体会全等图形就在我们身边.(准备直尺、网格纸片)全等图形的概念 阅读课本本课时“交流”前面的内容,感知全等图形.观察感知 它们的形状、大小都分别 相同 ,分别能完...(全国地区适应) 图片预览:   篇15:青岛版数学八年级上册3.2 分式的约分 课件(共14张PPT)点此进入下载文字摘要:(共14张PPT)第三章 分式3.2 分式的约分1.类比分数的约分,知道分式约分的意义与理论依据;2.能熟练地找到分子与分母的公因式,将分式进行约分;(重点)3.知道最简分式的意义.联想分数的约分,你能想出如何对分式进行约分吗?( )( )与分数约分类似,关键是要找出分式的分子与分母的公因式.像这样,根据分式的基本性质,把一个分式的分子与分母中1以外的公因式约去,叫做分式的约分.提示:分式的约分,一般要约去分子和分母所有的公因式,使所得的结果成为最简分式或整式.与最简分数的意义类似,当一个分式的分子与分母,除去1以外没有其他的公因式,这样的分式叫...(青岛市地区适应) 图片预览:  篇16:7.8 实数 第1课时 课件(共14张PPT)青岛版数学八年级下册点此进入下载文字摘要:(共14张PPT)第七章 实数7.8 实数第1课时1.了解实数的含义,能对实数进行分类;2.了解实数与数轴上点的一一对应关系,并能用数轴上的点表示无理数,同时掌握简单的无理数大小比较.实数的含义:有理数和无理数统称为实数.这样,我们认识的数的范围又一次扩大了,我们可以将实数按如下方式分类:有理数无理数实数正无理数负无理数正有理数负有理数零有限小数或无限循环小数无限不循环小数(一)实数的含义及分类如果按照数的正、负、零,可将实数分为三类,然后再按照是否有理数细分:正实数负实数负有理数正有理数0负无理数正无理数0正实数负实数实数典型例题...(青岛市地区适应) 图片预览:  篇17:青岛版八年级数学上册3.4 分式的通分 课件 (共14张PPT)点此进入下载文字摘要:(共14张PPT)第三章 分式3.4 分式的通分准确确定分式的最简公分母,熟练进行分式的通分.(重点)通分:思考:分式也可以进行通分吗?ac( )ab( )与分数的通分类似,根据分式的基本性质,使分子、分母同乘适当的整式,把分母不相同的分式变成分母相同的分式,这种变形叫分式的通分.如分式 与 分母分别是b,c,通分后分母都变成了bc.提示:与异分母分数的通分类似,异分母分式的通分关键是确定它们的公分母,通常取各分母系数的最小公倍数与所有字母因式的最高次幂的积作公分母,叫做最简公分母.注意:确定最简公分母是通分的关键.例1. 求下列各题的最简公分母:(...(青岛市地区适应) 图片预览:  篇18:15.2.1分式的乘除 课件(共24张PPT) 人教版八年级数学上册点此进入下载文字摘要:(共24张PPT)第15章 分式15.2.1 分式的乘除(1)1.理解并掌握分式的乘除法则。2.应用法则进行计算,能解决一些与分式有关的实际问题。学习目标知识回顾1.化简 正确的是( )A.-ab B.ab C.a2-b2 D.b2-a22.下列各式中,正确的是( )知识回顾知识回顾化简观察下列运算:分数乘除法计算法则内容你还清楚吗?问题引入读书独学一个水平放置的长方体容器,其容积为V,底面的长为a,宽为b,当容器内的水占容积的 时,水面...(全国地区适应) 图片预览:   篇19:7.8 实数 第1课时 课件(共15张PPT) 青岛版数学八年级下册点此进入下载文字摘要:(共15张PPT)第七章 实数7.8 实数第1课时1.了解实数的概念,会对实数进行分类.2.能求实数的相反数和绝对值.3.知道实数与数轴上的点一一对应,会比较两个实数的大小.知识回顾1.什么是有理数?有理数怎样分类?2.什么是无理数?带根号的数都是无理数吗?无理数是无限不循环小数.带根号的数不一定是无理数.整数分数有理数正有理数负有理数有理数0实数的概念:有理数和无理数统称为实数.活动:小组合作讨论,完成下列问题.任务一:对实数进行分类.问题:请你按照不同的分类标准对实数进行分类.有理数无理数实数正无理数负无理数正有理数负有理数零有...(青岛市地区适应) 图片预览:   Tags:八年级,数学课件,ppt,课件,19篇  |
21世纪教育网,教育资讯交流平台