篇1:2023年高考数学一轮复习圆锥曲线专题-圆锥曲线几何性质精华 讲义2023年高考数学一轮复习圆锥曲线专题-圆锥曲线几何性质精华 讲义资料可供全国地区适用。
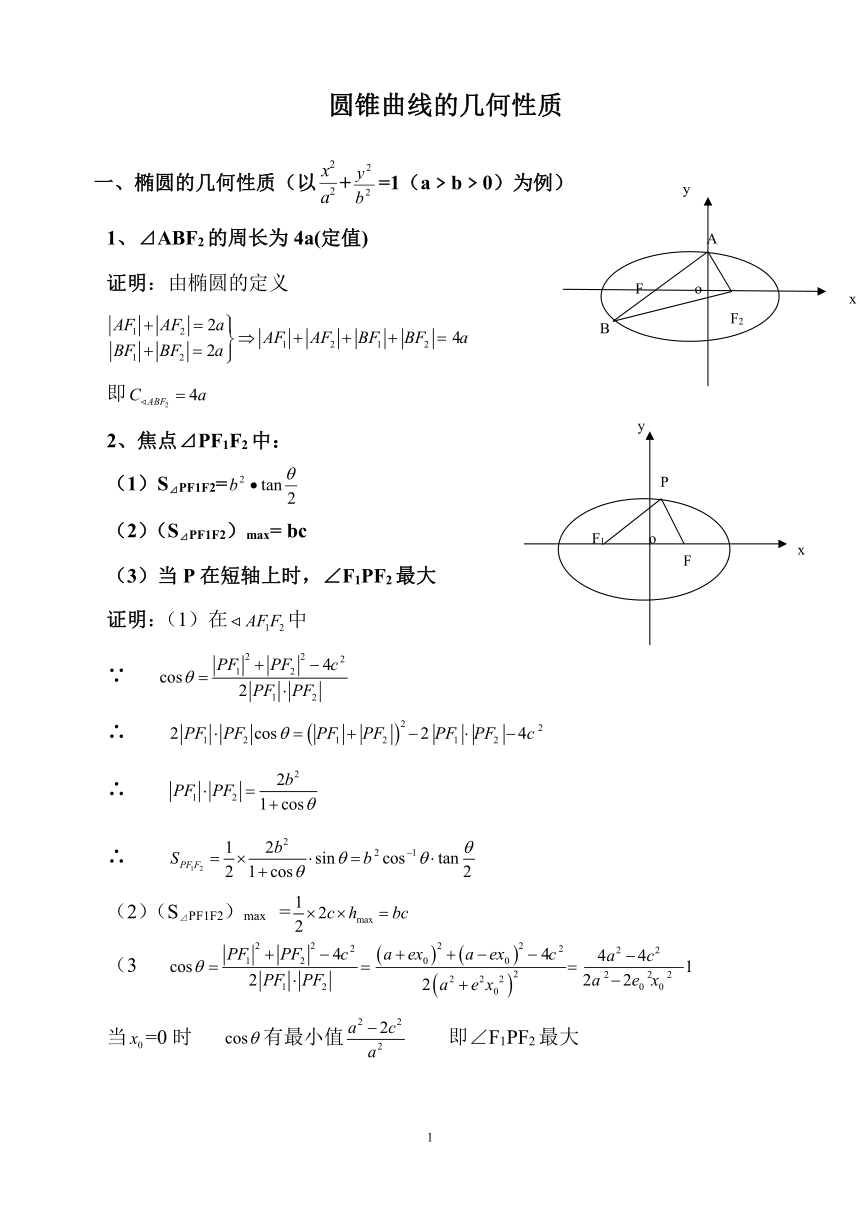
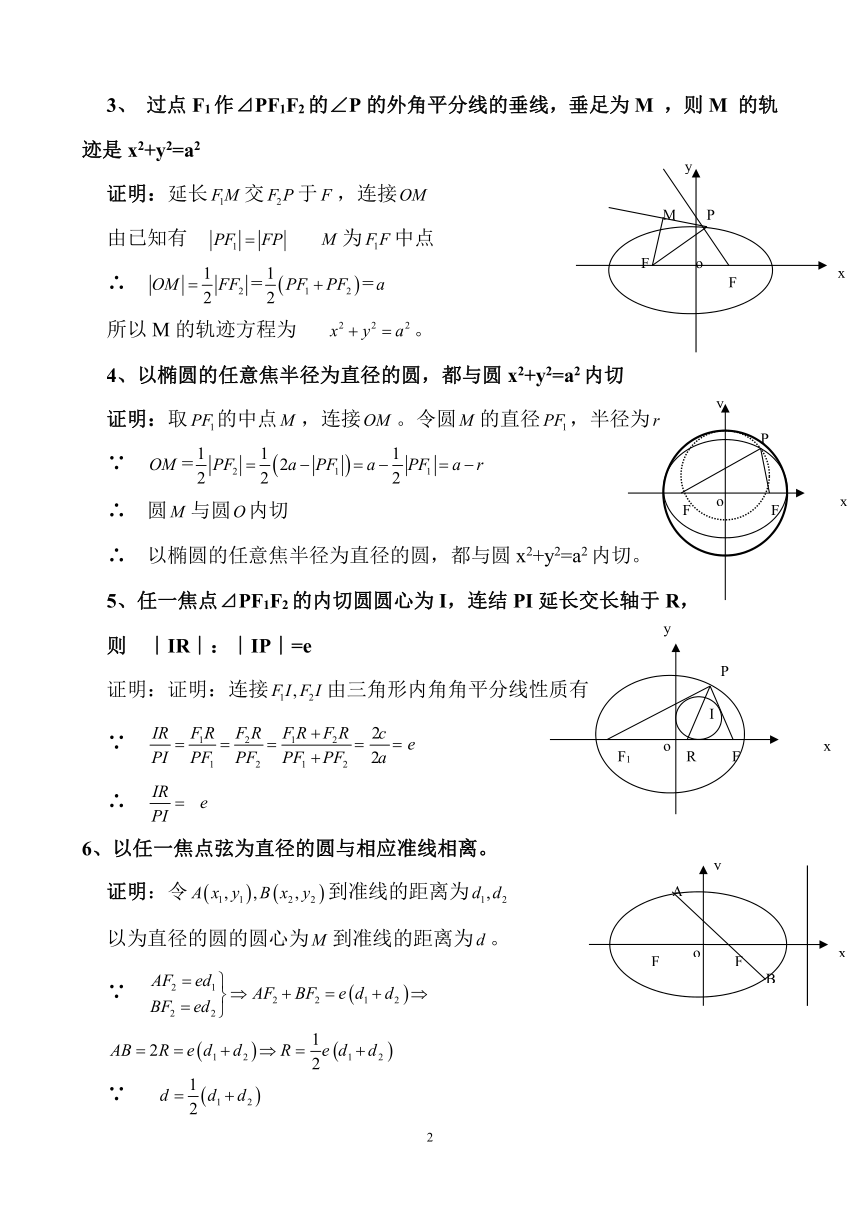
大致详情:圆锥曲线的几何性质一、椭圆的几何性质(以+=1(a﹥b﹥0)为例)1、⊿ABF2的周长为4a(定值)证明:由椭圆的定义即2、焦点⊿PF1F2中:(1)S⊿PF1F2=(2)(S⊿PF1F2)max= bc(3)当P在短轴上时,∠F1PF2最大证明:(1)在中∵∴∴∴(2)(S⊿PF1F2)max =(3当=0时 有最小值 即∠F1PF2最大3、 过点F1作⊿PF1F2的∠P的外角平分线的垂线,垂足为M ,则M 的轨迹是x2+y2=a2证明:延长交于,连接由已知有 为中点∴ ==所以M的轨迹方程为 。4、以椭圆的任意焦半径为直...
图片详情:
  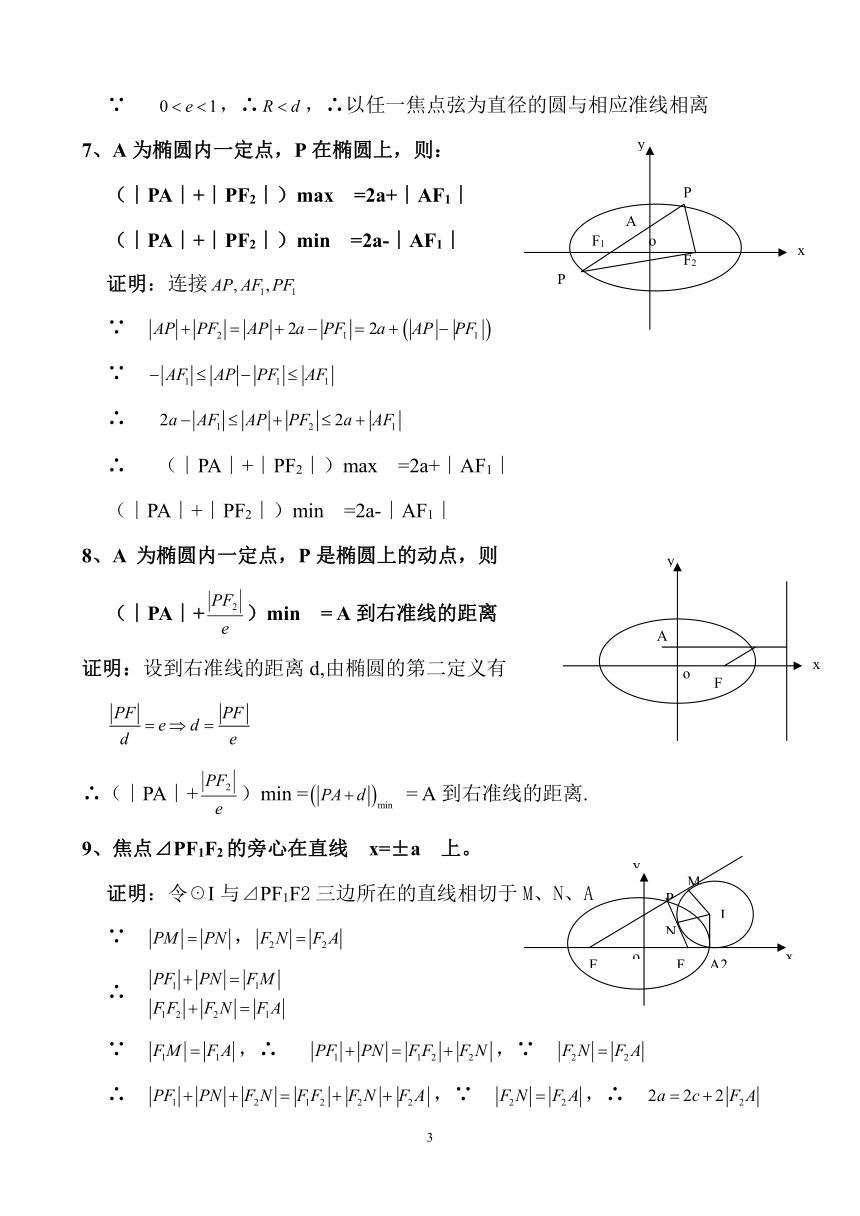   篇2:专题十二 圆锥曲线的求值与求轨迹问题 学案专题十二 圆锥曲线的求值与求轨迹问题 学案资料可供全国地区适用。
大致详情:中小学教育资源及组卷应用平台高中数学重难点突破专题十二 圆锥曲线的求值与求轨迹问题知识归纳一、椭圆秒杀小题常用结论(1)椭圆定义:|MF1|+|MF2|=2a(2a>|F1F2|).如图(1) 图(1) 图(2) 图(3) 图(4)(2)点P(x0,y0)和椭圆+=1(a>b>0)的关系P(x0,y0)在椭圆内 +<1;P(x0,y0)在椭圆上 +=1;P(x0,y0)在椭圆外 +>1.(3)如图(5),椭圆的通径(过焦点且垂直于长轴的弦)长为|AB|=,通径是最短的焦点弦.过焦点最长弦为长轴.过原点最长弦为长轴长2...
图片详情:
 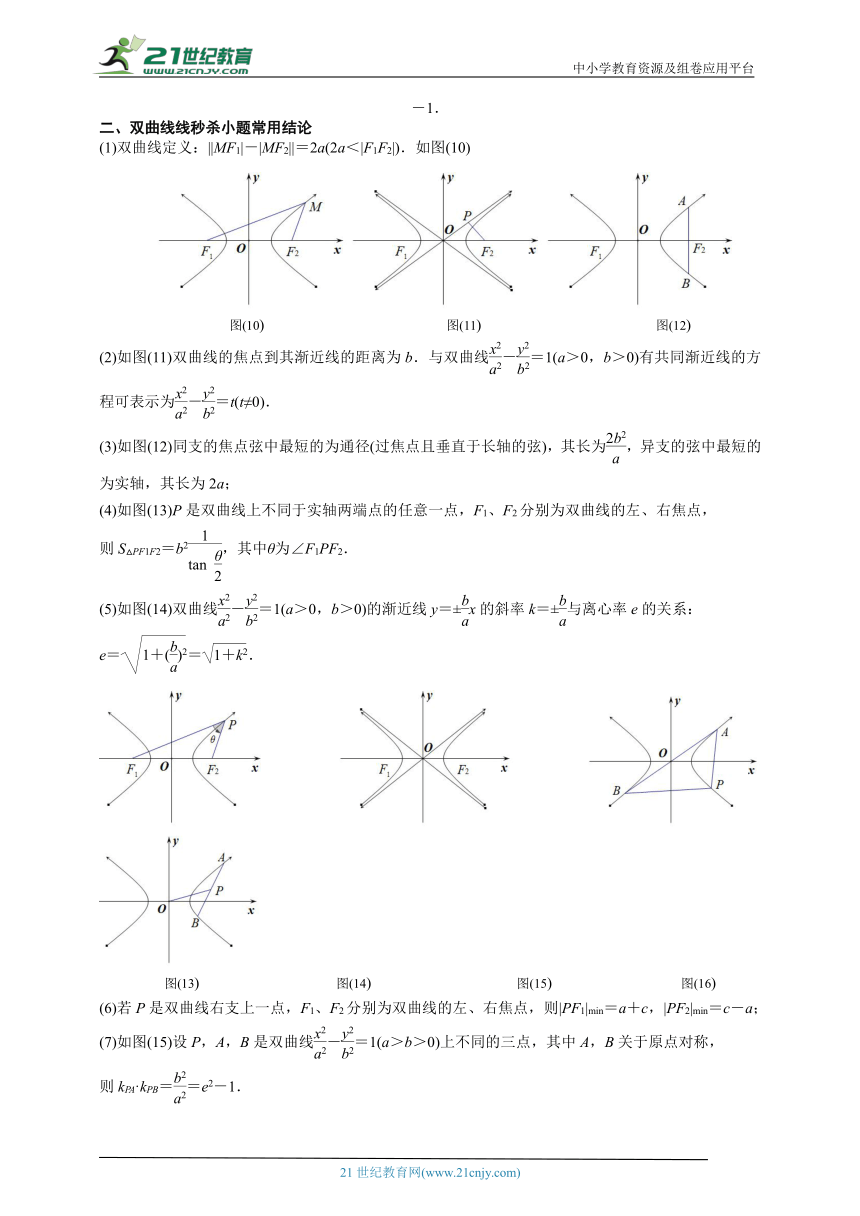 篇3:2023年高考数学一轮复习圆锥曲线专题-圆锥曲线轨迹方程的求法2023年高考数学一轮复习圆锥曲线专题-圆锥曲线轨迹方程的求法资料可供全国地区适用。
大致详情:圆锥曲线轨迹方程的求法 0603班 杨金梅 指导老师 陈引兰一直以来,圆锥曲线这部分内容都是高考必考内容,作为解析几何中一个重要的部分,在历次考试中也是让相当一部分考生感到棘手。现在,我就圆锥曲线的轨迹方程的问题作一个归纳总结。在一般情况下,我们对于求圆锥曲线的轨迹方程采用的方法有:直接法,定义法,相关点法,参数法。下面就以上几种方法作一下介绍。1、 用直接法求轨迹方程利用动点运动的条件作出等量关系,表示成x,y的等式。例:已知点A(-2,0),B(3,0).动点P(x,y)满足 PA· PB =x2,则点P的轨迹是( ).A、圆 B、椭圆 C、双曲线 D、抛物线...
图片详情:
   篇4:专题十三 圆锥曲线中的最值与范围问题 学案专题十三 圆锥曲线中的最值与范围问题 学案资料可供全国地区适用。
大致详情:中小学教育资源及组卷应用平台高中数学重难点突破专题十三 圆锥曲线中的最值与范围问题典例分析几何法解决的最值模型【例1-1】过椭圆+=1的中心任作一直线交椭圆于P,Q两点,F是椭圆的一个焦点,则△PFQ的周长的最小值为( )A.12 B.14 C.16 D.18【例1-1】答案 D 解析 由椭圆的对称性可知,P,Q两点关于原点对称,设F′为椭圆另一焦点,则四边形PFQF′为平行四边形,由椭圆定义可知:|PF|+|PF′|+|QF|+|QF′|=4a=20,又|PF|=|QF′|,|QF|=|PF′|,∴|PF|+|QF|=10,又PQ为...
图片详情:
   篇5:2023年高考数学一轮复习圆锥曲线专题-圆锥曲线定比弦的存在定理2023年高考数学一轮复习圆锥曲线专题-圆锥曲线定比弦的存在定理资料可供全国地区适用。
大致详情:圆锥曲线定比弦的存在定理摘要 本文研究了圆锥曲线中过定点并以此点为定比分点的弦的存在问题,给出了圆锥曲线中定比弦存在的较为一般的判定定理。关键词 圆锥曲线 定点 中点弦 定比弦The Existence Theroem of Fixed proportionNypothenuse in Conical CuryeCao Houliang(Class 9702,Department of Mathematics,Hubei Normal University)AbstractIn this paper,we carry out a research into the exi...
图片详情:
  篇6:2022-2023学年苏教版(2019)选择性必修一第三章 圆锥曲线与方程 单元测试卷(含解析)2022-2023学年苏教版(2019)选择性必修一第三章 圆锥曲线与方程 单元测试卷(含解析)资料可供全国地区适用。
大致详情:苏教版(2019)选择性必修一第三章 圆锥曲线与方程 单元测试卷学校:___________姓名:___________班级:___________考号:___________一、选择题1、过抛物线的焦点F且斜率为1的直线交抛物线C于A、B两点,抛物线的准线为l,于,于,则四边形的面积为( )A.32 B. C.64 D.2、已知O为坐标原点,垂直抛物线的轴的直线与抛物线C交于A,B两点,,则,则( )A.4 B.3 C.2 D.13、设抛物线的焦点为F,A为抛物线上一点且A在第一象限,,现将直线AF绕点F逆时针旋转30°得到直线l,且直线l与抛物线交于C,D两点,则(...
图片详情:
    篇7:2023年高考数学一轮复习 圆锥曲线专题-圆锥曲线问题通法通解(含答案)2023年高考数学一轮复习 圆锥曲线专题-圆锥曲线问题通法通解(含答案)资料可供全国地区适用。
大致详情:解圆锥曲线问题常用方法【学习要点】解圆锥曲线问题常用以下方法:1、数形结合法解析几何是代数与几何的一种统一,常要将代数的运算推理与几何的论证说明结合起来考虑问题,在解题时要充分利用代数运算的严密性与几何论证的直观性,尤其是将某些代数式子利用其结构特征,想象为某些图形的几何意义而构图,用图形的性质来说明代数性质。如“2x+y”,令2x+y=b,则b表示斜率为-2的直线在y轴上的截距;如“x2+y2”,令,则d表示点P(x,y)到原点的距离;又如“”,令=k,则k表示点P(x、y)与点A(-2,3)这两点连线的斜率……2、参数法(1)点参数利用点在某曲线上设点(常设“主动点”),以此...
图片详情:
    篇8:2023年高考数学一轮复习 圆锥曲线专题-圆锥曲线性质一览表 素材2023年高考数学一轮复习 圆锥曲线专题-圆锥曲线性质一览表 素材资料可供全国地区适用。
大致详情:圆锥曲线性质一览表性质 椭圆 双曲线 抛物线定义 {P||PF1|+|PF2|=2a} {P|||PF1|-|PF2||=2a} {P|=e (e=1)}{P|=e (0
图片详情:
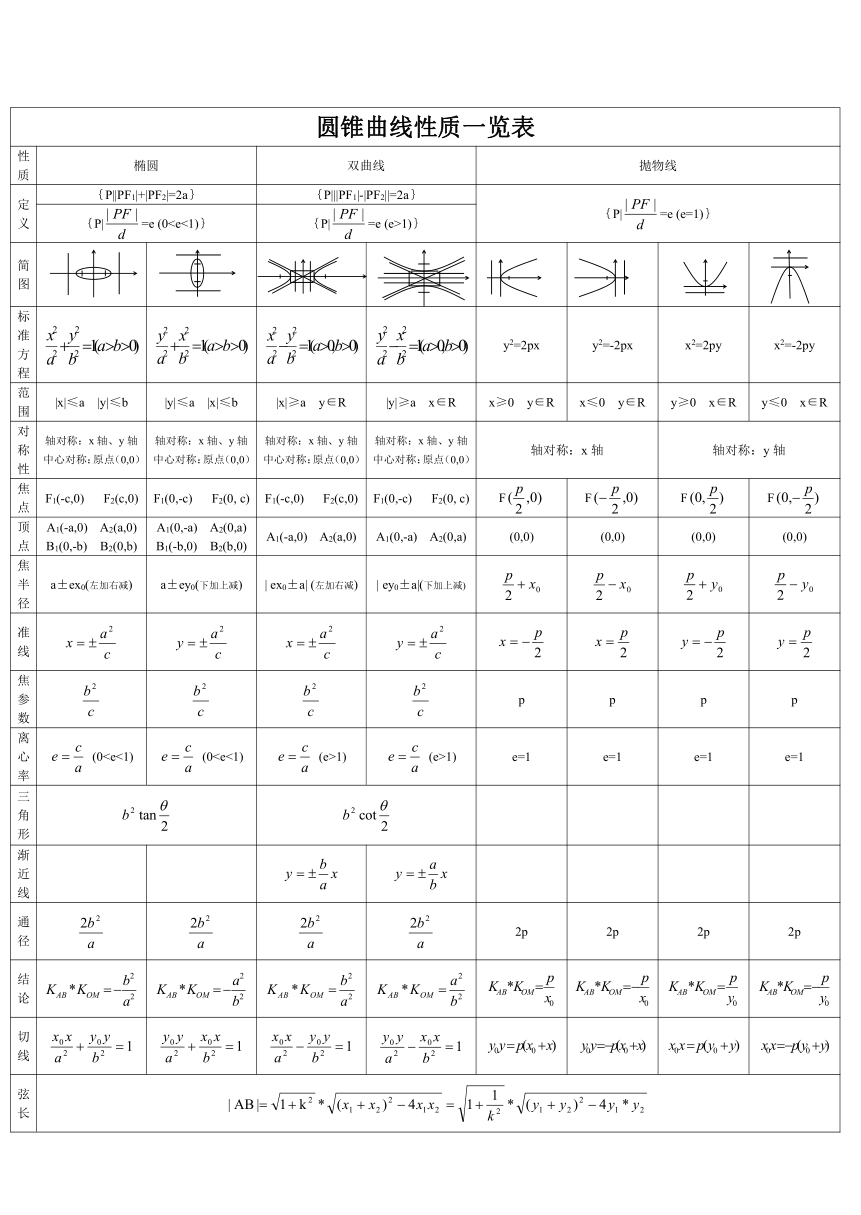 篇9:圆锥曲线综合专题训练(Word含解析)圆锥曲线综合专题训练(Word含解析)资料可供全国地区适用。
大致详情:圆锥曲线综合专题训练及解析一.选择题1.动点P到两定点F1(-4,0),F2(4,0)的距离之和为10,则动点P的轨迹方程是( )A.+=1 B.+=1 C.+=1 D.+=1【答案】B【解析】由已知得c=4,2a=10即a=5,b2=a2-c2=9,故选B.2.(2022.乙卷)设F为抛物线的焦点,点A在C上,点,若,则( )A.2 B. C.3 D.【答案】B【解析】由已知得p=2,F(1,0),|AF|=|BF|=2,即点A到抛物线C得准线x=-1的...
图片详情:
   篇10:专题十四 圆锥曲线中的二级定理及其应用 学案专题十四 圆锥曲线中的二级定理及其应用 学案资料可供全国地区适用。
大致详情:中小学教育资源及组卷应用平台高中数学重难点突破专题十四 圆锥曲线中的二级定理及其应用知识归纳一、椭圆与双曲线焦点三角形的性质1、椭圆焦点三角形的性质(1)椭圆焦点为,,P为椭圆上的点,,则;(2).(3).(注意:r为内切圆半径)2、双曲线焦点三角形性质(1)双曲线焦点为F1、F2,为双曲线上的点,,则(2)(3)(4)内切圆的圆心横坐标一定等于;证明:如图,;3、共焦点的椭圆与双曲线的焦点三角形已知椭圆C1:+=1(其中a>b>0)与双曲线C2:-=1(其中m>0,n>0)共焦点,e1,e2分别为C1,C2的离心率,M是C1,C2的一个交点,θ=∠F1M...
图片详情:
  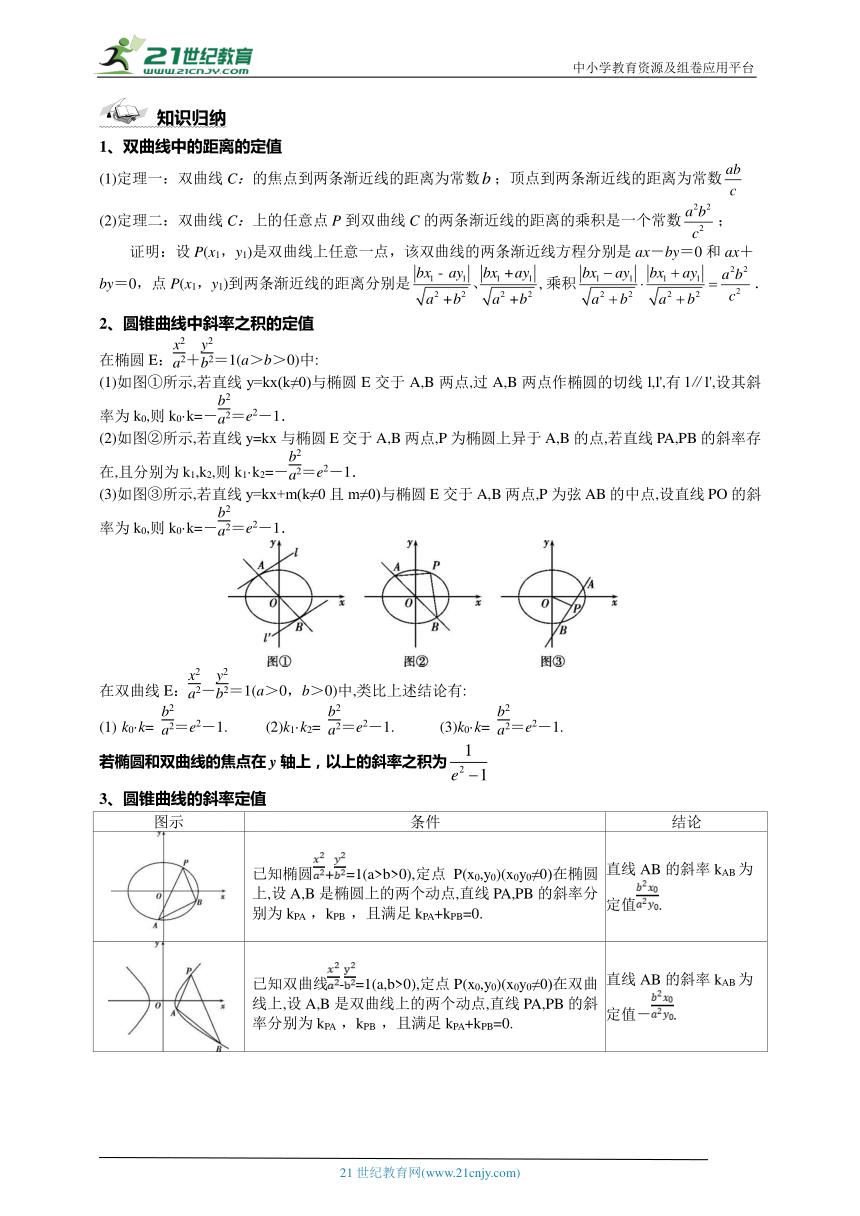  篇11:高中数学人教A版(2019)选择性必修一圆锥曲线的方程单元测试高中数学人教A版(2019)选择性必修一圆锥曲线的方程单元测试资料可供全国地区适用。
大致详情:登录二一教育在线组卷平台 助您教考全无忧高中数学人教A版(2019)选择性必修一圆锥曲线的方程单元测试一、单选题1.(2021高二下·怀化期末)已知抛物线 : ,则( )A.它的焦点坐标为 B.它的焦点坐标为C.它的准线方程是 D.它的准线方程是【答案】B【知识点】抛物线的简单性质【解析】【解答】抛物线 : ,则 ,它的焦点坐标为 ,它的准线方程是 。故答案为:B.【分析】将抛物线的方程转化为抛物线的标准方程,从而确定焦点和准线的位置,进而求出焦点的坐标和准线方程。2.(2021高二下·普宁期末)已知双曲线 (a>0,b>0)的两条渐近线斜率分别为...
图片详情:
  篇12:圆锥曲线选择填空专项训练(含答案)圆锥曲线选择填空专项训练(含答案)资料可供全国地区适用。
大致详情:绝密★启用前平面解析几何圆锥曲线专项练习考试范围:平面解析几何;考试时间:120分钟注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)一、单选题1.椭圆的左顶点为A,点P在C上且在第二象限,点P关于x轴,y轴的对称点分别为,Q,直线的斜率分别为,若,则C的离心率为( )A. B. C. D.2.油纸伞是中国传统工艺品,使用历史已有1000多年.以手工削制的竹条做伞架,以涂刷天然防水桐油的皮棉纸做伞面.油纸伞是世界上最早的雨伞,纯手工制成,全部取材于天然,是中国古人智慧的结晶.在某市开展的油纸伞文化艺术节中,某油...
图片详情:
   篇13:2023年高考数学一轮复习 圆锥曲线专题-圆锥曲线中常见不等关系的确立 素材2023年高考数学一轮复习 圆锥曲线专题-圆锥曲线中常见不等关系的确立 素材资料可供全国地区适用。
大致详情:圆锥曲线中常见不等关系的确立圆锥曲线中的范围问题,是一个难点问题,这类问题涉及的知识范围广,条件隐含,能力要求高,同学们对这类问题往往思路不清,不会建立元素之间的关系(不等关系),本文将介绍解决这类问题的几种常用方法,供同学们在复习中参考。一、利用点与曲线的位置关系建立不等关系例1、已知椭圆C的方程试确定m的取值范围,使得对于直线,在椭圆C上有不同的两点关于该直线对称。分析:由题可得关于直线对称的两点P、Q的中点在直线上,且PQ所在的直线与的交点在椭圆的内部,利用点在椭圆的内部求解。解析:设是椭圆C上的关于直线对称的不同的两点,M(x,y)是弦PQ的中点,因为点P,Q都在椭圆上,故有...
图片详情:
 篇14:圆锥曲线结论圆锥曲线结论资料可供全国地区适用。
大致详情:椭圆椭圆方程的定义:平面内与两个定点、的距离的和等于常数(大于)的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点的距离叫椭圆的焦距。若P为椭圆上任意一点,则有|PF1|+|PF2|=2a2、①椭圆的标准方程:i. 中心在原点,焦点在x轴上:ii. 中心在原点,焦点在轴上:.②一般方程:③方程的轨迹为椭圆.3、性质: ①顶点:或. ②轴:对称轴:x轴,轴;长轴长,短轴长.③焦点:或 .④焦距:..⑥离心率:.且越接近,对应的椭圆越扁;反之,越接近于,这时椭圆越接近于圆。⑦范围:由标准方程知,,说明椭圆位于直线,所围成的矩形里;4、焦半径:i、设为椭圆...
图片详情:
  篇15:2023年高考数学一轮复习圆锥曲线专题-圆锥曲线中存在点关于直线对称问题 讲义2023年高考数学一轮复习圆锥曲线专题-圆锥曲线中存在点关于直线对称问题 讲义资料可供全国地区适用。
大致详情:圆锥曲线中存在点关于直线对称问题对于此类问题有第一种通法,即抓住两点对称中体现的两要点:垂直(斜率之积为-1)和两点连线中点在对称直线上,至于参数的范围则是由联立后方程的△产生,下面举例说明:例1:已知椭圆C:3x2+4y2=12,试确定m的取值范围,使得对于直线l:y=4x+m,椭圆C上有不同两点关于这条直线对称.解:设存在两点A(x1,y1)、B(x2,y2)关于l对称,中点为C(x0,y0),则AB所在直线为y=-x+b.与椭圆联立得:x2-2bx+4b2-12=0,∴ x0= = ,y0= = EQ \F(-x1+b-x2+b,2) = .∵ C在y=4x+m上...
图片详情:
 Tags:圆锥曲线,单元,测试,精选,15篇

|
21世纪教育网,教育资讯交流平台