篇1:2.2导数的概念及其几何意义 同步练习(Word版含解析)2.2导数的概念及其几何意义 同步练习(Word版含解析)资料可供全国地区适用。
大致详情:课时作业(十五) 导数的概念及其几何意义[练基础]1.某汽车的紧急刹车装置需在遇到紧急情况2 s内完成刹车,其位移(单位:m)关于时间(单位:s)的函数为s(t)=t3-4t2+20t+15,则s′(1)的实际意义为( )A.汽车刹车后1 s内的位移B.汽车刹车后1 s内的平均速度C.汽车刹车后1 s时的瞬时速度D.汽车刹车后1 s时的位移2.如图,直线l是曲线y=f(x)在x=4处的切线,则f′(4)=( )A. B.3C.4 D.53.已知曲线y=f(x)在点(1,f(1))处的切线方程为2x-y+2=0,则f′(1)=( )A.4 B.-4...
图片详情:
  篇2:数学人教A版(2019)选择性必修第二册5.1.2 导数的概念及其几何意义 课件(共20张ppt)数学人教A版(2019)选择性必修第二册5.1.2 导数的概念及其几何意义 课件(共20张ppt)资料可供全国地区适用。
大致详情:(共20张PPT)5.1.2 导数的概念及其几何意义前面我们研究了两类变化率问题:一类是物理学中的问题, 涉及平均速度和瞬时速度; 另一类是几何学中的问题, 涉及割线斜率和切线斜率 . 这两类问题来自不同的学科领域, 但在解决问题时, 都采用了由“平均变化率”逼近“瞬时变化率”的思想方法 ; 问题的答案也是一样的表示形式 . 下面我们用上述思想方法研究更一般的问题.对于函数y=f(x), 设自变量x从x0变化到x0+ x, 相应地,函数值y就从f(x0)变化到f(x0+ x).这时,x的变化量为 x , y的变化量为 y=f(x0+ x)-f(x0).我们把比值,即= 叫做函...
图片详情:
  篇3:数学人教A版(2019)选择性必修第二册5.1.1导数的概念及其意义 课件(共18张ppt)数学人教A版(2019)选择性必修第二册5.1.1导数的概念及其意义 课件(共18张ppt)资料可供全国地区适用。
大致详情:(共18张PPT)第五章 一元函数的导数及其应用为了描述现实世界中的运动、变化现象, 在数学中引入了函数. 刻画静态现象的数与刻画动态现象的函数都是数学中非常重要的概念 . 在对函数的深入研究中 , 数学家创立了微积分 , 这是具有划时代意义的伟大创造 , 被誉为数学史上的里程碑.微积分的创立与主要与处理四类科学问题直接相关. 一是已知物体运动的路程作为时间的函数, 求物体在任意时刻的速度与加速度, 反之, 已知物体的加速度作为时间的函数, 求速度与路程; 二是求曲线的切线; 三是求已知函数的最大值与最小值; 四是求长度、面积、体积和重心等.历史上的科学家们对这些问题的兴趣和研究经久...
图片详情:
    篇4:人教版高中数学选择性必修第二册5.1.2导数的概念及其几何意义第1课时 同步作业(含解析)人教版高中数学选择性必修第二册5.1.2导数的概念及其几何意义第1课时 同步作业(含解析)资料可供全国地区适用。
大致详情:人教版高中数学选择性必修第二册5.1.2导数的概念及其几何意义第1课时 同步作业(原卷版)1.在求平均变化率时,自变量的增量Δx应满足( )A.Δx>0 B.Δx<0C.Δx=0 D.Δx≠02.函数在某一点的导数是( )A.在该点的函数的增量与自变量增量的比B.一个函数C.一个常数,不是变数D.函数在这一点到它附近一点之间的平均变化率3.若函数f(x)=x2的图象上有一点P(2,4)及邻近点Q(2+Δx,4+Δy),则 =( )A.4 B.4xC.4+2(Δx)2 D.4+2Δx4.已知函数f(x)=-x2+x,则f(x)从-1到-...
图片详情:
   篇5:人教版高中数学选择性必修第二册5.1.2导数的概念及其几何意义第2课时 同步作业(含解析)人教版高中数学选择性必修第二册5.1.2导数的概念及其几何意义第2课时 同步作业(含解析)资料可供全国地区适用。
大致详情:人教版高中数学选择性必修第二册5.1.2导数的概念及其几何意义第2课时 同步作业(原卷版)1.设f′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )A.不存在 B.与x轴平行或重合C.与x轴垂直 D.与x轴斜交2.已知函数y=f(x)的图象如右图所示,则f′(xA)与f′(xB)的大小关系是( )A.f′(xA)>f′(xB)B.f′(xA) 图片详情:
    篇6:5.1.2导数的概念及其几何意义 导学案(Word版无答案)5.1.2导数的概念及其几何意义 导学案(Word版无答案)资料可供全国地区适用。
大致详情:5.1.2 导数的概念及其几何意义【学习目标】1. 经历由平均变化率到瞬时变化率的过程,体会导数的概念的实际背景.2.了解导函数的概念,理解导数的几何意义.【自主学习】知识点:一、导数1、平均变化率对于函数,自变量x从x0变化到x0+△x,相应地,函数值y就从f(x0)变化到f(x0+△x)。这时,x的变化量为△x,y的变化量为△y=f(x0+△x)—f(x0)。我们把比值,即=______________叫做函数从x0到x0+△x的平均变化率。2、导数的概念:如果当△x→0时,平均变化率无限趋近于一个确定的值,即有极限,则称在x=x0处可导,并把这个确定的值叫做在x=...
图片详情:
  篇7:数学人教A版(2019)选择性必修第二册5.1.2导数的概念及其几何意义 课件(共17张ppt)数学人教A版(2019)选择性必修第二册5.1.2导数的概念及其几何意义 课件(共17张ppt)资料可供全国地区适用。
大致详情:
图片详情:
  篇8:人教A版(2019)选择性必修第二册第五章一元函数的导数及其应用5.1导数的概念及其意义5.1.2导数的概念及其几何意义(word版含解析)人教A版(2019)选择性必修第二册第五章一元函数的导数及其应用5.1导数的概念及其意义5.1.2导数的概念及其几何意义(word版含解析)资料可供全国地区适用。
大致详情:人教A版(2019) 选择性必修第二册 第五章 一元函数的导数及其应用 5.1 导数的概念及其意义 5.1.2 导数的概念及其几何意义一、单选题1.已知函数在处的切线方程过,则函数的最小值为( )A. B.1 C. D.2.已知曲线y=,则曲线的切线斜率取得最小值时的直线方程为( )A.x+4y-2=0 B.x-4y+2=0 C.4x+2y-1=0 D.4x-2y-1=03.已知曲线在点处切线的倾斜角为,则角是( )A.锐角 B.直角 C.钝角 D.零度角4.函数与的图象如下图,则函数的图象可能是( )A.B.C....
图片详情:
 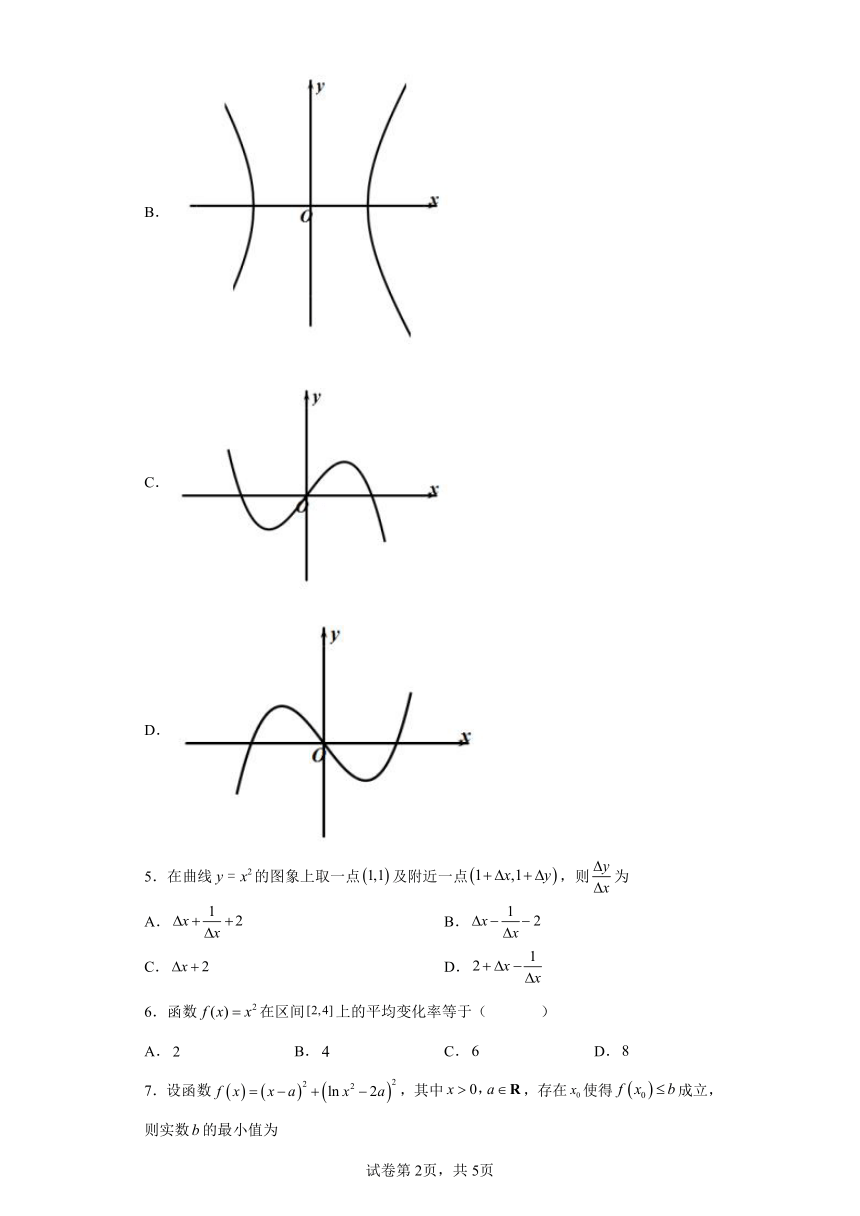   篇9:2023-2024学年高中数学人教A版选修二 5.1 导数的概念及其意义 同步练习2023-2024学年高中数学人教A版选修二 5.1 导数的概念及其意义 同步练习资料可供全国地区适用。
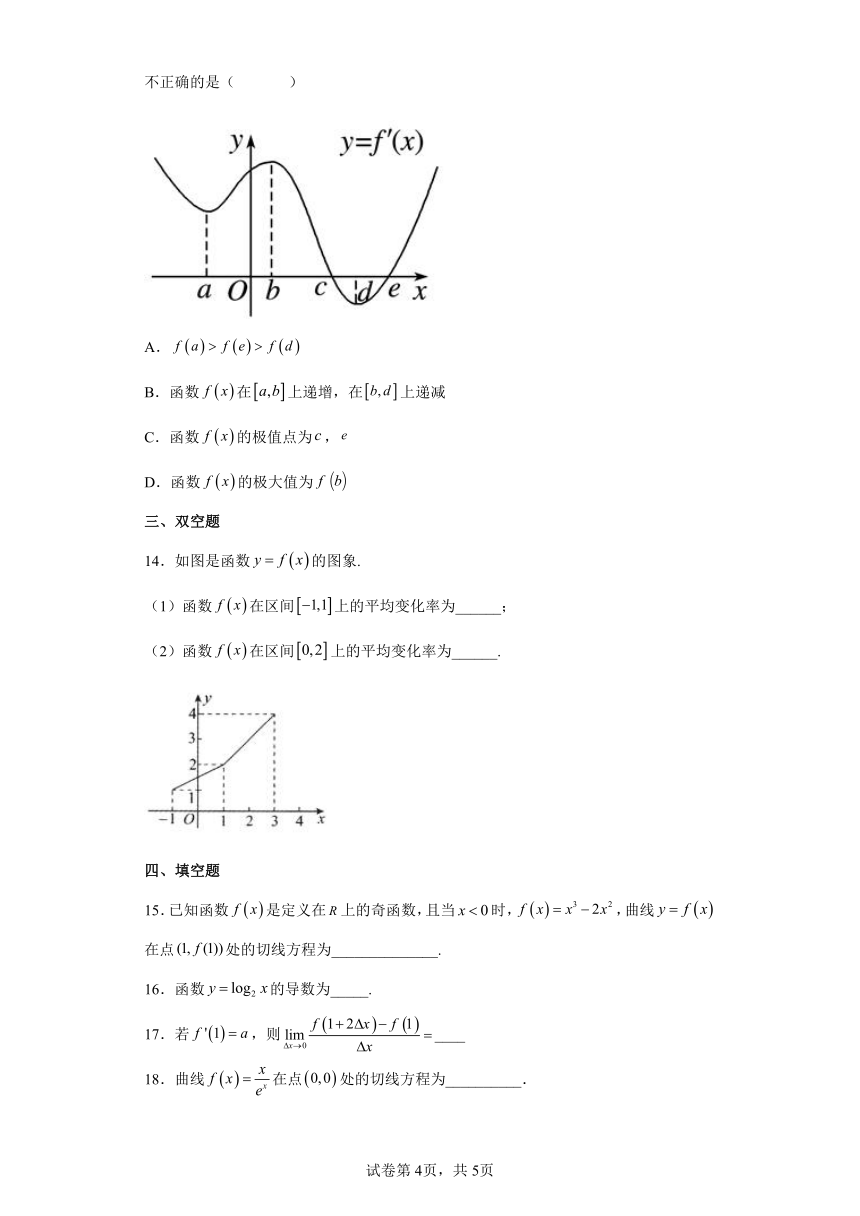
大致详情:2023-2024学年高中数学人教A版选修二 5.1 导数的概念及其意义 同步练习一、选择题1.(2023高二下·安徽月考)若曲线的一条切线的斜率是,则切点的横坐标为( )A.1 B. C. D.【答案】B【知识点】导数的几何意义【解析】【解答】设切点的横坐标为x,则,解得或x=-1(舍去).故选:B.【分析】 设出切点横坐标,求导,通过斜率得出横坐标方程,求解可得切点的横坐标 .2.(2023高二下·宝安期中)某物体的运动路程单位:与时间单位:的关系可用函数表示,则该物体在时的瞬时速度为( )A. B. C. D.【答案】D【知识点】变化的快慢与变化率【解析】【...
图片详情:
  篇10:人教A版(2019)选择性必修第二册 5.1导数的概念及其意义 教案(表格式)人教A版(2019)选择性必修第二册 5.1导数的概念及其意义 教案(表格式)资料可供全国地区适用。
大致详情:课题:导数的概念一、教学内容解析《导数的概念》是高中数学的一节概念课.数学学习离不开推理,推理离不开判断,而判断是以一切概念为基础的.因此,数学教师必须要重视概念的教学.导数以高起点,高观点和更一般的方法简化了中学数学中许多与函数相关的问题.导数的出现也为我们今后微积分的发展提供了方法和工具,从而使得它在其它学科领域也有了广泛的应用.但我们又不能将导数作为一种规则和步骤来学习,否则,学生很难体会导数的思想及其内涵,这样导数概念的学习就至关重要.一般地,导数概念学习的起点是极限,但就高中学生的认知水平而言,他们很难理解极限的形式化定义.因此,我们对导数概念的引入从变化率入手,用形象直观的...
图片详情:
  Tags:导数,概念,及其,意义,ppt

|
21世纪教育网,教育资讯交流平台