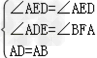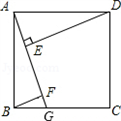
试题：“四边形abcd是正方形”的答案及解答过程

日期:2015-2-10 14:58 阅读:

题文

如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于E，BF∥DE，交AG于F．

（1）求证：AF﹣BF=EF；

（2）将△ABF绕点A逆时针旋转，使得AB与AD重合，记此时点F的对应点为点F'，若正方形边长为3，求点F'与旋转前的图中点E之间的距离．

21教育网答案：

（1）证明：如图，∵正方形ABCD，

∴AB=AD，∠BAD=∠BAG+∠EAD=90°，

∵DE⊥AG，

∴∠AED=90°，

∴∠EAD+∠ADE=90°，

∴∠ADE=∠BAF，

又∵BF∥DE，

∴∠AEB=∠AED=90°，

在△AED和△BFA中，

∵

，

∴△AED≌△BDA（AAS），

∴BF=AE，

∴AF﹣AE=EF，

∴AF﹣BF=EF；

（2）解：如图，

根据题意知：∠FAF'=90°，DE=AF'=AF，

∴∠F'AE=∠AED=90°，即∠F'AE+∠AED=180°，

∴AF'∥ED，

∴四边形AEDF'为平行四边形，又∠AED=90°，

∴四边形AEDF'是矩形，

∴EF'=AD=3．

Tags：试题,四边形,abcd,正方形,答案

图文推荐

相关文章