|
有学生问小编一道关于数学正弦定理的数学题,题目如下: 在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b﹣c)cosA﹣acosC=0, (Ⅰ)求角A的大小; (Ⅱ)若 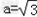 , ,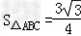 ,试判断△ABC的形状,并说明理由. ,试判断△ABC的形状,并说明理由.那么关于这样的正弦的题,可以怎么处理呢?看看21教育名师怎么解这个题目吧: 解:(Ⅰ)∵(2b﹣c)cosA﹣acosC=0,由正弦定理, 得(2sinB﹣sinC)cosA﹣sinAcosC=0, ∴2sinBcosA﹣sin(A+C)=0,sinB(2cosA﹣1)=0, ∵0<B<π, ∴sinB≠0, ∴ 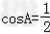 , ,∵0<A<π, ∴ 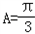 .. ..(Ⅱ)∵ 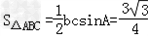 , ,即 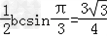 ∴bc=3① 由余弦定理可知cosA= 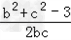 = = ∴b2+c2=6,② 由①②得 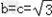 , ,∴△ABC为等边三角形. Tags:abc...,方法,解题,定理,正弦

|
21世纪教育网,教育资讯交流平台




