九年级上册数学(人教版)课后答案第25章·习题24.2答案

九年级上册数学(人教版)其余更多章节的课后答案，请点此查看>>>九年级上册数学(人教版)课后答案汇总<<<

1.解：（1）点P在⨀O内.   （2）点P在⨀O上.   （3）点P在⨀O外.   

2.提示：（1）相离.   （2）相切.   （3）相交.

3.解：（1）因为VU是⨀T的切线，U为切点，所以UT ⊥UV，所以∠VUT=90〬.在Rt△UVT中，∠UVT=90〬,UV=28cm， TU=25cm，所以VT²=UV²+TU²,即VT²=28²+25², 所以VT=√(〖28〗^2+〖25〗^2 )=√1409(cm).
           （2）因为VU与VW均是⨀T的切线，所以∠UVT=∠TVW，∠TWV=90〬. 又因为∠UVW=60 〬，所以∠TVW = 1/2×60 〬=30 〬.在Rt△TVW中，∠TWV=90〬，  ∠TVW =30 ，TW=25cm，所以TV=2WT=2×25=50（cm）.

4.证明：连接OC. ∵OA=OB, ∴△OAB为等腰三角形，又∵CA=CB，∴OC⊥AB. ∵AB经过⨀O的半径OC的外端C，并且垂直于半径OC，∴AB是⨀O的切线.

5.证明：连接OP，因为AB是小圆O的切线，P为切点，所以OP⊥AB，又AB是大圆O的弦，所以由垂径定理可知AP=PB.

6.解：因为PA，PB是⨀O的切线，所以PA=PB，∠ PAB=∠PBA.又由题意知OA ⊥ PA，∠OAB=25〬,所以∠PAB=90〬-25〬=65〬.所以∠P=180〬-2∠PAB=180〬-65〬×2=50〬.

7.解：半径为4cm的圆可以做两个，半径为3cm的圆只能作一个，不能作出同时经过A,B两点，且半径为2cm的圆.

8.提示：锐角三角形的外心在这个三角形的内部；直角三角形的外心在这个直角三角形的斜边的中点；钝角三角形的外心在这个三角形的外部.

9.提示：可以在车轮上任意连接两点，作出它的中垂线，重复一次，则这两条中垂线的交点即为圆心，从而可确定它的半径.

10.解：设圆心为O，如图48所示，连接OW,OX,因为YW,YX均是⨀O的切线，W,X均为切点，所以OW⊥WY,OX⊥XY. 又因为XY⊥WY,所以∠OWY=∠OXY=∠WYX = 90 〬,所以四边形OXYW是矩形.又因为OW=OX,所以四边形OXYW是正方形，所以OW=WY=0.65m. 答：这个油桶的底面半径是哦0.65m.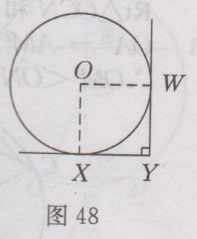

11.解：连接OE,OG,则OE ⊥AB,OG⊥CD,又因为AB//CD,所以点E,O,G在同一直线上.由AB,CD,BC均是⨀O  的切线，可得∠BOC=90〬. 在Rt△BOC中，OB=6cm，CO=8cm，所以BC=√(OB^2+OC^2 )=√(6^2+8^2 )=10(cm). 答：BC的长是10cm.

12.证明：连接OC, ∵CD为⨀O的切线，C为切点，∴OC ⊥CD. 又∵AD⊥CD∴AD// OC , ∴∠  DAC= ∠OCA. ∵OA=OC, ∴∠OAC= ∠OCA. ∴∠DAC=∠CAO,即AC平分∠DAB.

13.解：连接O₁B，O₁O₂，O₂A，O₂B. ∵两个圆是等圆，而⨀O ₁经过O ₂，故⨀O ₂过O₁,  ∴ O₁A=O₂A=O₁B=O ₂B=O₁O ₂，∴ 四边形AO ₁BO ₂是菱形，又O₁O ₂= O₁A，∴△O₁A O ₂是等边三角形，∴∠O₁A O ₂=60〬. ∵AB是菱形AO₁BO ₂的对角线，∴∠O₁AB=1/2∠O₁A O ₂=1/2×60〬=30〬.

14.解：如图49所示，连接OA,OB,OC,设  ⨀O 与AB,BC,CA的切点分别为D,E,F，连接OD,OE,OF，则OD ⊥AB,OE ⊥BC,OF ⊥AC,∴ S△ABC=S△AOB+S△BOC+S△AOC =1/2AB•OD +1/2 BC•OE+ 1/2 AC•OF=1/2 AB•r+ 1/2 BC•r+ 1/2 AC•r= 1/2 r(AB+BC+AC)=1/2 r(a+b+c)  , 又∵S△ABC= 1/2AC•BC=1/2 ab,∴1/2 r(a+b+c)=1/2ab, ∴ r=ab/(a+b+c).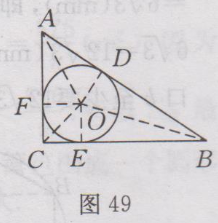

Tags：答案,九年级,上册,数学,人教