九年级上册数学(人教版)课后答案第25章·习题24.1答案

九年级上册数学(人教版)其余更多章节的课后答案，请点此查看>>>九年级上册数学(人教版)课后答案汇总<<<

1.已知：如图38所示，在⨀O中，AB为直径，CD为⨀O的任意一条弦（不是直径的弦）.求证：AB>CD.    

证明：连接OC,OD，在△OCD中，OC+OD>CD,即AB>CD.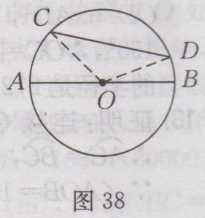

 

2.解：（1）∵OA,OB是⨀O的半径，∴OA=OB=50mm，又∵AB=50mm，∴OA= OB =AB，∴△AOB是等边三角形，∴∠AOB=60〬

           （2）过点O作OC⊥AB,垂足为点C，如图39所示，则∠OCA=90〬，由垂径定理得，AC=CB=1/2AB,∵AB=50mm，∴AC= 25mm.在Rt△OAC中，OC²=OA²-AC²=50²-25²=25²×3, ∴OC=  √(25²×3) = 25√3 (mm),即点O到AB的距离是25√3mm.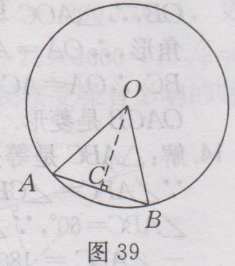

 

3.  解：∵⌒AB  =⌒AC , ∴AB=AC, ∴∠B=∠C=75〬，∴∠A=180〬-75〬-75〬=30〬.即∠A的度数是30〬.

 

4.   解：⌒AB  =⌒CD ,证明如下：∵AD=BC,∴⌒AD =⌒BC ,∴⌒AD +⌒AC  =⌒BC  +⌒AC ,即⌒DC = ⌒AB .

 

5.   解：如图40所示，连接OC . ∵ OA⊥BC , ∴ =⌒AB , ∴∠COA=∠AOB , ∵ ∠AOB =50〬，∴∠COA=50〬，∴∠ADC=1/2∠AOC=1/2×50〬=25〬，即∠ADC=25〬.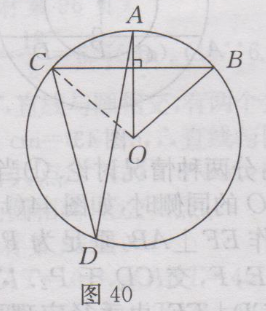

6.解：第二个（即中间的）工件是合格的，理由是90〬的圆周角所对的弦是直径.

 

7.已知：如图41所示，四边形ABCD为⨀O内接平行四边形，求证：◇ABCD为矩形.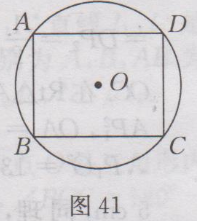   

证明：四边形ABCD为平行四边形，∴∠A=∠C.又∵四边形ABCD内接于⨀O，∴∠A+∠C=180〬，∴∠A=∠C=90〬，∴  ◇ABCD为矩形.   

 

8.解：如图42所示，连接OC，设⨀O的半径为r，∵M为CD的中点，∴OM⊥CD，∴CM=1/2CD=1/2×4=2cm.  在Rt△CMO中，OC²-OM²=CM²，即r²-(6-r)²=2²,  r²-(36-12r+ r²)=4，12r=40，r=10/3，∴⨀O的半径为10/3 cm.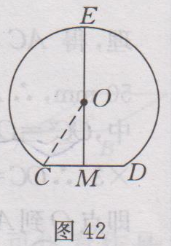

9.证明：如图43所示，过点O作OP⊥AB，垂足为点P，由垂径定理可知PA=PB，PC=PD，∴PA-PC=PB-PD，即AC=BD.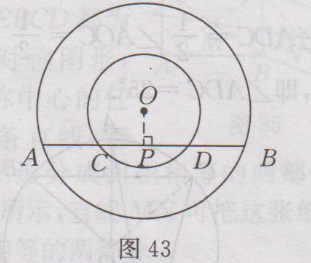

10.解：分两种情况讨论.①当AB、CD在点O的同侧时，如图44（1）所示，过点O作EF⊥AB，垂足为P₁，交⨀O于点E、F，交CD于P₂. ∵CD//AB，∴CD⊥EF，由垂径定理可知AP₁=BP₁=1/2AB=24×1/2=12(cm).   CP₂=DP₂=1/2CD=5(cm).  连接OA，OC.  在Rt△AOP₁中，P₁O²=OA²-AP₁²，OA=13cm，AP₁=12cm，∴P₁O ²=13²-12²=25 ，∴P₁O=5cm,   同理，OP₂=√(OC^2-CP₂²)=√(〖13〗^2-5^2 )=12(cm),  ∴P₁P₂=OP₂ - OP₁=12 -5=7（cm）.   ②当AB、CD在点O的两侧时，如图44（2）所示，与AB、CD在点O的同侧时的解法类似，可得OP₁=5cm ,  OP₂=12cm,  ∴P₁P₂= OP₁+ OP₂=5+12=17(cm) , 即AB与CD的距离为7cm或17cm.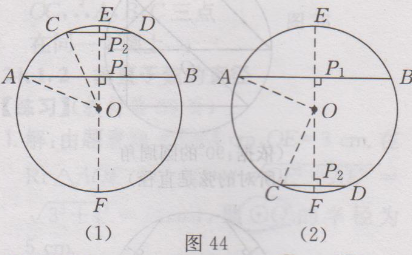

11.证明：∵AB//CD，⌒AC =⌒BD . 又∵MN是AB的垂直平分线，则有,MN过圆心O，是直径，∴⌒AM =⌒BM , ⌒AM -⌒AC =⌒BM -⌒BD ，即⌒CM =⌒DM ,  ∴MN垂直平分CD.

 

12.∵OC⊥AB,AB=300，∴由垂径定理，可知AD=DB=1/2AB=150，又∵CD=45，∴OD=OC-CD=OC-45，又∵OA,OC均为⨀O的半径，∴OA=OC，在Rt△AOD中，OA²=OD²+AD²，∴OC²=(OC-45)²+150²，∴OC=272.5（m）. 答：这段弯路的半径是272.5m.

 

13.证明：连接OC,∵C是⌒AB 的中点，∴⌒AC =⌒BC  ,∴∠AOC=∠BOC,又∵∠AOB=120〬, ∴∠AOC=∠BOC=1/2×120〬=60〬. 又∵OA=OC=OB, ∴△AOC与△BOC均是等边三角形，∴OA=AC=OC, BO=OC=BC, ∴OA=AC=BC=OB, ∴四边形OACB是菱形.

 

14.解：△ABC是等边三角形，证明如下：

∵∠APC=∠CPB=60〬，∴∠BAC=∠ABC=60〬，∵∠ACB=180〬-∠BAC-∠ABC = 180〬-60〬-60〬=60〬, ∴∠ABC=∠ACB=∠BAC,  ∴AB=BC=CA,∴△ABC是等边三角形.

 

15.解：OM<ON. 理由如下：如图45所示，连接OC,OA,则OA=OC. ∵ON⊥CD,OM⊥AB,∴CN=1/2CD,AM=1/2 AB,又∵CD<AB, ∴CN<AM, ∴CN²<AM².在Rt△OCN和Rt△OAM中，OM²=OA²-AM², ON²=OC²-CN²,∴OM²<ON²,∴OM<ON.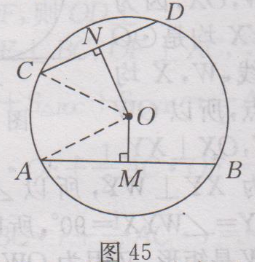

16.解：如图46所示，过点A作AB⊥ON,垂足为B,因为∠QON=30〬，OA=200m，∠OBA=90〬，所以AB=1/2OA=1/2×200=100(m),因为100m<200m，所以居民楼会受到噪音的影响.在MN上找到点C，使AC=200m，又OA=200m，则火车在铁路MN上沿ON方向行驶到点O处时，居民楼开始受到火车噪音的影响.由勾股定理，得OB²=OA²-AB²=200²-100²=30000，所以OB=100√3（m）,同理BC= 100√3（m），所以OC=OB+BC=100√3+100√3=200√3（m），又（200√3÷1000）÷72×3600=10√3≈17.3（s），所以居民楼受噪音影响的时间约为17.3s.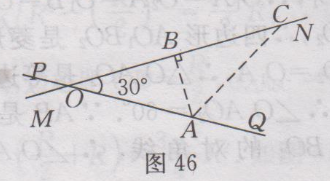

17.解：同弧所对的圆外角小于相应地圆周角，因此只要航行中保持∠XPY<∠XZY，就能保证点P在⌒XY 所在的圆外，也就保证了船只不进入浅滩.

Tags：答案,九年级,上册,数学,人教