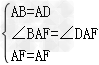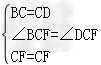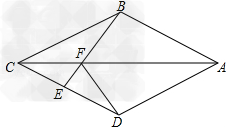
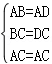
题目： 如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF． （1）证明：∠BAC=∠DAC，∠AFD=∠CFE． （2）若AB∥CD，试证明四边形ABCD是菱形； （3）在（2）的条件下，试确定E点的位置，∠EFD=∠BCD，并说明理由．  （1）证明：∵在△ABC和△ADC中 ，  ∴△ABC≌△ADC（SSS）， ∴∠BAC=∠DAC， ∵在△ABF和△ADF中 ，  ∴△ABF≌△ADF， ∴∠AFD=∠AFB， ∵∠AFB=∠AFE， ∴∠AFD=∠CFE； （2）证明：∵AB∥CD， ∴∠BAC=∠ACD， 又∵∠BAC=∠DAC， ∴∠CAD=∠ACD， ∴AD=CD， ∵AB=AD，CB=CD， ∴AB=CB=CD=AD， ∴四边形ABCD是菱形； （3）当EB⊥CD时，∠EFD=∠BCD， 理由：∵四边形ABCD为菱形， ∴BC=CD，∠BCF=∠DCF， 在△BCF和△DCF中 ，  ∴△BCF≌△DCF（SAS）， ∴∠CBF=∠CDF， ∵BE⊥CD， ∴∠BEC=∠DEF=90°， ∴∠EFD=∠BCD． Tags：四边形,abcd,ab,ad  |
21世纪教育网，面向全国的中小学学教师、家长交流平台
