|
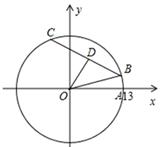
题目: 在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为____. 答案: ∵直线y=kx﹣3k+4必过点D(3,4), ∴最短的弦CD是过点D且与该圆直径垂直的弦。 ∵点D的坐标是(3,4),∴OD=5。 ∵以原点O为圆心的圆过点A(13,0)。 ∴圆的半径为13。∴OB=13。∴BD=12。 ∴BC的长的最小值为24。 考点梳理 点、线、圆与圆的位置关系: 点和圆位置关系 ①P在圆O外,则 PO>r。 ②P在圆O上,则 PO=r。 ③P在圆O内,则 0≤PO<r。 反过来也是如此。 直线和圆位置关系 ①直线和圆无公共点,称相离。 AB与圆O相离,d>r。 ②直线和圆有两个公共点,称相交,这条直线叫做圆的割线。AB与⊙O相交,d<r。 ③直线和圆有且只有一公共点,称相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点。AB与⊙O相切,d=r。(d为圆心到直线的距离) 圆和圆位置关系 ①无公共点,一圆在另一圆之外叫外离,在之内叫内含。 ②有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切。 ③有两个公共点的叫相交。两圆圆心之间的距离叫做圆心距。 设两圆的半径分别为R和r,且R〉r,圆心距为P,则结论:外离P>R+r;外切P=R+r;内含P<R-r; 内切P=R-r;相交R-r<P<R+r。 圆的计算公式: 1.圆的周长C=2πr=或C=πd 2.圆的面积S=πr2 3.扇形弧长L=圆心角(弧度制)× r = n°πr/180°(n为圆心角) 4.扇形面积S=nπ r2/360=Lr/2(L为扇形的弧长) 5.圆的直径 d=2r 6.圆锥侧面积 S=πrl(l为母线长) 7.圆锥底面半径 r=n°/360°L(L为母线长)(r为底面半径) 圆的方程: 1、圆的标准方程:在平面直角坐标系中,以点O(a,b)为圆心,以r为半径的圆的标准方程是 (x-a)2+(y-b)2=r2。 特别地,以原点为圆心,半径为r(r>0)的圆的标准方程为x2+y2=r2。 2、圆的一般方程:方程x2+y2+Dx+Ey+F=0可变形为(x+D/2)2+(y+E/2)2=(D2+E2-4F)/4.故有: ①当D2+E2-4F>0时,方程表示以(-D/2,-E/2)为圆心,以(√D2+E2-4F)/2为半径的圆; ②当D2+E2-4F=0时,方程表示一个点(-D/2,-E/2); ③当D2+E2-4F<0时,方程不表示任何图形。 3、圆的参数方程:以点O(a,b)为圆心,以r为半径的圆的参数方程是 x=a+r*cosθ, y=b+r*sinθ, (其中θ为参数) 圆的端点式:若已知两点A(a1,b1),B(a2,b2),则以线段AB为直径的圆的方程为 (x-a1)(x-a2)+(y-b1)(y-b2)=0 圆的离心率e=0,在圆上任意一点的曲率半径都是r。 经过圆x2+y2=r2上一点M(a0,b0)的切线方程为 a0·x+b0·y=r2 在圆(x2+y2=r2)外一点M(a0,b0)引该圆的两条切线,且两切点为A,B,则A,B两点所在直线的方程也为 a0·x+b0·y=r2。
Tags:平面,直角,坐标系,xoy,原点

|
21世纪教育网,教育资讯交流平台