九年级上册数学(人教版)课后答案第25章·习题24.3答案

九年级上册数学(人教版)其余更多章节的课后答案，请点此查看>>>九年级上册数学(人教版)课后答案汇总<<<

1.解：填表如下：

   

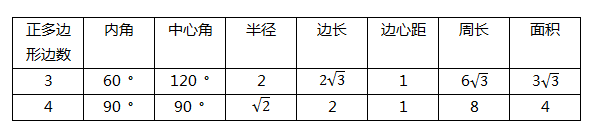2.解：如图52所示，连接AC，∵∠D=90〬, ∴  AC为直径.在Rt△ACD中，AC=√(a^2+a^2 )=√2 a,∴  半径至少为√2/2a.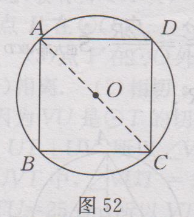

3.  解：正多边形都是轴对称图形.当正多边形的边数为奇数时，对称轴条数与正多边形边数相等，是正多边形顶点与对边中点所在的直线；当正多边形的边数为偶数时，它的对称轴条数也与边数相等，分别是对边中点所在的直线和相对顶点所在的直线.正多边形不都是中心对称图形.当正多边形边数为偶数时，它是中心对称图形，对称中心是正多边形的中心；当正多边形的边数为奇数时，它不是中心对称图形.

4.   证明：∵ ABCDE为正五边形，∴ AB=BC=AE ,  ∠A= ∠B= ∠C. 又∵ L,H,I分别为AE,AB,BC边中点，∴  AL=AH=BH=BI=IC, ∴  △AHL≌△BIH≌△CJI, ∴ HL=HI=IJ .  ∠AHL=∠BHI=∠BIH=∠CIJ, ∠LHI=180〬-∠AHL-∠BHI, ∠HIJ=180〬-∠BIH-CIJ, ∴∠LHI=∠HIJ.同理：LK=KJ=IJ=HI=HL, ∠HLK=∠LKJ=∠KJI=∠LHI=∠HIJ. ∴五边形HIJKL是正五边形.

5.  解：如图53所示，连接BF,过点A作AG ⊥  BF ,垂足为点G, 因为∠BAF=120〬，所以∠BAG=60〬，所以∠ABG=∠30〬.在Rt△ABG中，AB=12cm，∠AGB=90〬，∠ABG=30〬，所以AG=1/2AB=1/2×12=6（cm）.由勾股定理，得BG= √(AB^2-AG^2 ) =√(〖12〗^2-6^2 )=6√3(mm),即b=BF=2BG=2×6√3=12√3(mm).答：扳手张开的开口b至少要12√3mm.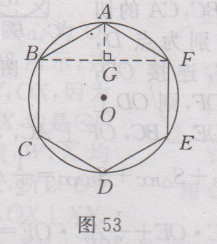

6.  解：设剪去的小直角三角形的两直角边长分别为xcm，xcm,由题意可知（4-2x）²=x²+x².解得x₁=4+2√2，x₂=4-2√2.因为x<4，所以x=4+2√2不符合题意，舍去，所以x=4-2√2.所以4-2x=4-2(4-2√2)=(4√2-4)cm,即这个正八边形的边长是(4√2-4) （cm），S正八边形=S正方形-4S小三角形=4²-4×1/2•x•x=16-2(4-2√2)²= 16 -2 (24-16√2) =（32√2-32） cm^2.  答：这个正八边形的边长为(4√2-4)cm，面积是（32√2-32）cm².   

7.  解：①当用48cm长的篱笆围成一个正三角形时，边长为48÷3=16（m）,此时 S△=1/2×16×8√3=64√3（m²）.
             ②当围成一个正方形时，边长为48÷4=12（m），此时S正方形=12×12=144（m²）.
             ③当围成一个正六边形时，边长为48 ÷6=8 （m),此时S正六边形=6×1/2  ×8 ×4√3=96√3 （m^2 ）.
             ④当围成一个圆时，圆的半径为48/2π = 24/π （m）,此时，S圆=π（24/π）^2=576/π （m^2 ）.因为64√3<144<96√3<576/π，所以S圆最大. 答：用48cm长的篱笆围成一个圆形的绿化场地面积最大.

8.  提示：圆外切正三角形的边长为2√3R；圆外切正四边形的边长为2R；圆外切正六边形的边长为(2√3)/3R.

Tags：答案,九年级,上册,数学,人教