|
为了帮助同学们的学习,下面是21世纪教育网为大家整理的人教版八年级下册数学同步作业本课后答案第3章·18.2特殊的平行四边形答案,答案仅供同学们参考使用,小编建议同学们自行完成作业后再对照答案,这样更有利于同学们的成绩提升! 人教版八年级下册数学同步作业本其余更多章节的课后答案,请点此查看>>>人教版八年级下册数学同步作业本课后答案汇总<<< 下面是小编整理的: (课后答案查找—扫码关注) 同步学习 (一) 1、D 2、C 3、10 4、5 5、设AB = x,则BD = 4 + x,由勾股定理, 得x² + 8² = (x + 4)²,解得x = 6,即AB的长度为6 cm. 由S△ABD = AB·AD = AE·BD,可得AE = 4.8,即点A到BD的距离为4.8 cm. (二) 1、C 2、C 3、∠A = 90°或者AC = BD 4、BC = 2AB 5、(1)∵ 四边形ABCD是平行四边形, ∴ AO = CO,BO = DO ∵ △AOB是等边三角形, ∴ AO = BO. ∴ AC = BD. ∴ □ABCD是矩形 (2)由△AOB是等边三角形,且AB = 4, 得AC = 2AO = 2AB = 8.由勾股定理,得BC = 4 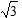 ∴ S□ABCD = 4 × 4 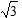 =16 =16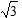 (cm²) (cm²) (三) 1、A 2、C 3、96 cm²;4OCm 4、2.4 cm 5、提示:先证△CBE ≌ △CDE, ∴ ∠CBE = ∠CDE,再由AB∥CD, ∴ ∠AFD = ∠CDE, ∴ ∠AFD = ∠CBE (四) 1、D 2、B 3、连接AC,BD ∵ E,F,G,H分别是AD,AB,BC,CD的中点, ∴ EF ∥= ½BD,GH ∥= ½BD,EH ∥= ½AC,FG ∥= ½AC. 由矩形ABCD,可得AC = BD, ∴ EF = FC = GH = EH, ∴ 四边形EFGH是菱形. 4、提示:由四边形ABCD是平行四边形,且EF垂直平分AC,可证△AOE ≌ △COF, ∴ EO = FO.又AO = CO, ∴ 四边形AFCE是平行四边形.再由AC ⊥ EF,可得□AFCE是菱形. (五) 1、B 2、C 3、3;3 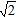 , ,4、75° 5、(1)提示:由四边形ABCD是正方形,且DE = BF,可证△ADE ≌ △ABF, ∴ ∠EAD = ∠FAB ∵ ∠EAD + ∠EAB = 90°, ∴ ∠FAB + ∠EAB = 90°, ∴ AE ⊥ AF (2)提示:由(1)可得AE ⊥ AF,且AE = AF.由勾股定理, 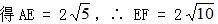 (六) 1、D 2、一个角是直角且一组邻边相等,或者对角线垂直且相等. 3、提示:由四边形ABCD是正方形,可得AO = BO = CO = DO,AC ⊥ BD、又E,F,G,H分别是OA,OB,OC,OD的中点,可得EO = FO = GO = HO. ∴ 四边形EFGH是矩形.又EG ⊥ FH, ∴ 四边形EFGH是正方形. 4、提示:作BF ⊥ DC,交DC的延长线于点F. 先证四边形BEDF是正方形,得BE = ED = DF = FB = 4. 再证△ABE ≌ △CBF, ∴ 四边形ABCD的面积等于正方形BEDF的面积16. 能力提升 1 - 4 C A C C 5、12 6、12 7、(1)提示:证明DE = DC,DF = DC (2)当D为AC的中点时,四边形AECF为矩形(理由略) 8、提示:连接AC、由四边形ABCD为菱形,且∠B = 60°, 可得△ABC和△ACD为等边三角形,从而可证△ABE ≌ △ACF, ∴ AE = AF.又∠EAF = 60°, ∴ △AEF为等边三角形. 9、提示:连接PC.由正方形ABCD,可得△ABP ≌ △CBP, ∴ AP = CP.再证四边形PECF是矩形, ∴ PC = EF, ∴ AP = EF. 10、(1)MN = DM提示:在AD上取中点F,连接MF,证明△DFM ≌ △MBN,即可得DM = MN. (2)MN = DM仍成立.提示:在AD上取一点P,使DP = MB,连接MP,证明△DPM ≌ △MBN即可. Tags:答案,人教,八年级,下册,数学

|
21世纪教育网,教育资讯交流平台




