沪科版八年级下册数学课时学练课后答案第17章·活页单元测试卷17.3一元二次根式的判别 ...

沪科版八年级下册数学课时学练其余更多章节的课后答案，请点此查看>>>沪科版八年级下册数学课时学练课后答案汇总<<<

课时达标

1、D       2、A       3、A        4、 1/4  

5、 3（答案不唯一，所填写的数值只要满足m2＜12即可）

6、题目略
（1）k＞-9/4  
（2）若k是负整数，则k只能为-1或-2，如果k=-2,原方程x²-3x+1=0，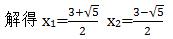

 

课后作业

1、B       2、B         3、A  

4、m＜-5/4  

5、±2  

6、 3  

7、（1）原方程由两个不相等的实数根。
       （2）原方程有两个不相等的实数根  
       （3）原方程由两个相等的实数根  

8、解：因为关于x的方程x2-4x+b=0有两个相等的实数根，所以△=（-4）²-4b=0,所以b=4又因为a=1,c=4,所以b=c=4，所以△ABC为等腰三角形。   

9、解：
（1）因为△=[2（k-1）] ²-4（k²-1）=4k²-8k+4-4k²+4=-8k+8,又因为原方程由两个不相等的实数根，所以-8k+8＞0,解k＜1,即实数k的取值范围是k＜1    

（2）假设0是方程的一个跟=根，则代入原方程，得0²+2（k-1）×0+k²-1=0,解得k=-1或k=1（舍去），即当k=-1时，0就为原方程的一个根，此时原方程变为x²-4x=0，解得x1=0,x2=4，所以它的另一个根是4.

10、证明：△=9（m-1）²-4×2（m²-4m-7）=m²+14m+65=（m+7）²+16,因为对于任何实数m，都有（m+7）²≥0,所以（m+7）²+16＞0,所以△＞0，即原方程有两个不相等的实数根，所以方程2x²+3（m-1）x+m²-4m-7对于任何实数m，永久由两个不相等的实数根。

11、解：∵关于x的一元二次方程kx²-2（k+2）x+k+5=0没有实数根，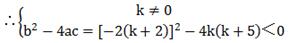

解得k＞4,当k=5时，方程（k-5）x²-2（k+2）x+k=0为一元二次方程，此时方程的根为x=5/114，当k≠5时，方程（k-5）x²-2（k+2）x+k=0为一元二次方程，

∴b²-4ac=[-2（k+2）] ²-4（k-5）×k=4（9k+4）,

∵k＞4且k≠5,   ∴4（9k+4）＞0,即b²-4ac＞0,   ∴此时方程必有实数根。

综上所述，关于x的方程（k-5）x²-2（k+2）x+k=0必有实数根  

12、D  13、C  14、C 

Tags：活页,判别,根式,二次,一元