篇1:第一章 解三角形 单元测试卷B(解析版)第一章 解三角形 单元测试卷B(解析版)资料可供全国地区适用。
大致详情: 解三角形单元测试卷(B)一、单选题1.在中,角的对边分别为,已知,且,点满足,,则的面积为( )A. B. C. D.2.在ΔABC中,a,b,c分别为角A,B,C所对的边,b=c,且满足.若点O是ΔABC外一点,∠AOB=θ(),OA=2,OB=4,则平面四边形OACB面积的最大值( )A. B. C. D.3.已知ABC的三边,,满足:,则此三角形是( )A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰直角三角形4.在中,,若点P是所在平面内任意一点,则的取值范围是( )A. B. C. D.5.设分别是的三边长,且,则的...
图片详情:
   篇2:2023届考前小题专攻 专题二 三角函数、解三角形 第二讲三角恒等变换与解三角形 课件(共28张PPT)2023届考前小题专攻 专题二 三角函数、解三角形 第二讲三角恒等变换与解三角形 课件(共28张PPT)资料可供全国地区适用。
大致详情:(共28张PPT)第二讲 三角恒等变换与解三角形微专题1微专题2微专题1常考常用结论1.两角和与差的正弦、余弦、正切公式(1)sin (α±β)=sin αcos β±cos αsin β.(2)cos (α±β)=cos αcos β sin αsin β.(3)tan (α±β)=.2.二倍角的正弦、余弦、正切公式(1)sin 2α=2sin αcos α.(2)cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.(3)tan2α=.3.常用公式(1)降幂扩角公式:cos2α=,sin2α=.(2)升幂公式:1+cos 2α=2cos2...
图片详情:
    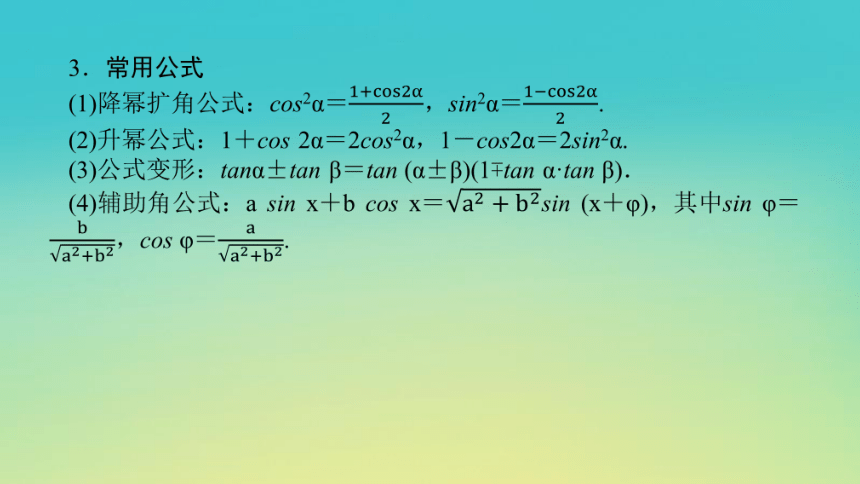 篇3:【初中几何一题多解】第3章 解三角形(含解析)【初中几何一题多解】第3章 解三角形(含解析)资料可供全国地区适用。
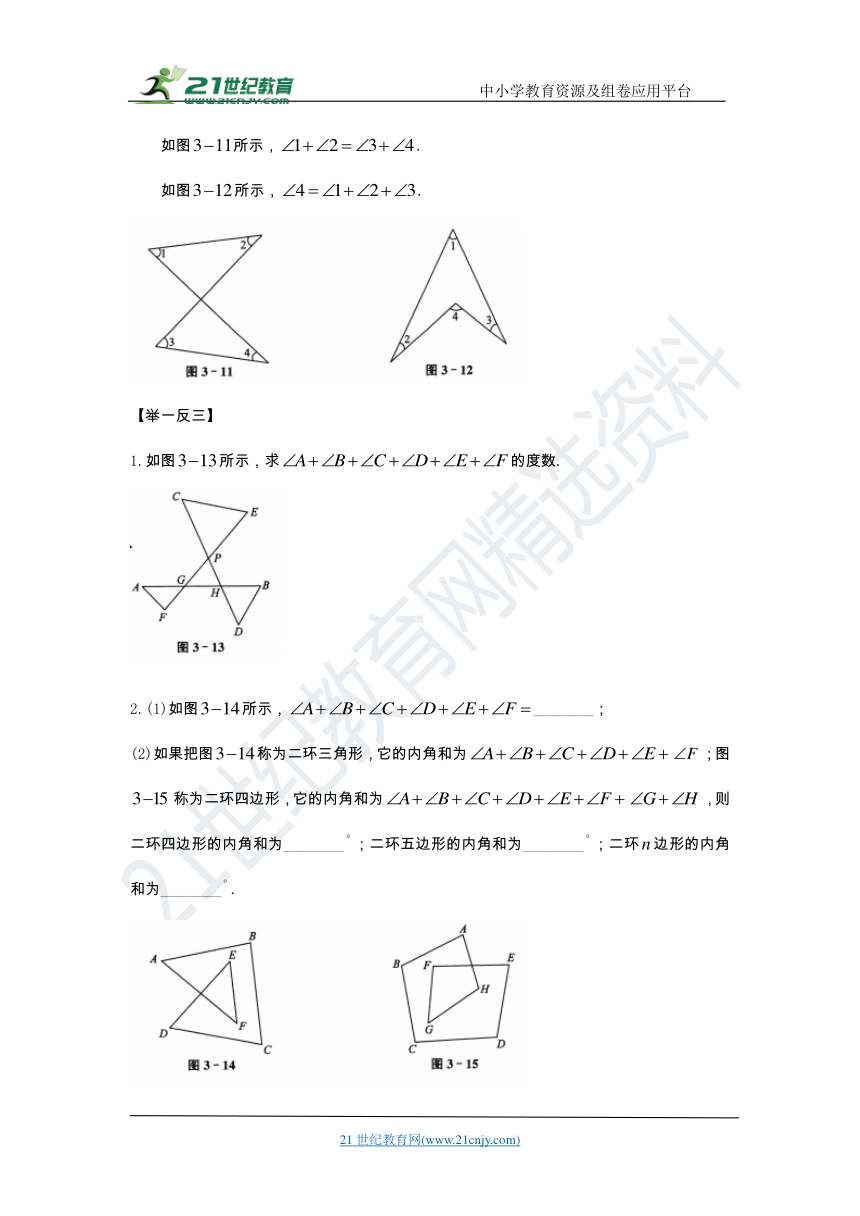
大致详情:第3章 解三角形第1题如图所示,在凹四边形$ABDC$中,求证:.【解题策略】利用三角形内角和定理或三角形外角性质来证明.【证法一】如图所示,连接.在中,,即.在中,,【证法二】如图所示,连接并延长.是的外角,同理,.∴.即.【证法三】如图所示,延长,交于点.是的外角,是的外角,∴∴.【解后反思】三角形内角和定理及三角形外角性质是研究图形中各角数量关系的重要衣据,在研究复杂图形中角与角的数量关系时,关键是能够从中分解出三角形、四边形或“飞镖图”(图3-1)这样的基本图形,同时联系外角与内角的关系.【举一反三】1.如图所示,平分平分.设,求(用含的式子表示...
图片详情:
     篇4:2023届考前小题专攻 专题二 三角函数、解三角形 第三讲三角函数与解三角形 课件(共23张PPT)2023届考前小题专攻 专题二 三角函数、解三角形 第三讲三角函数与解三角形 课件(共23张PPT)资料可供全国地区适用。
大致详情:(共23张PPT)第三讲 三角函数与解三角形大题一般为两问:第一问一般为利用正、余弦定理实施“边角互化”求角,多与三角形的内角和定理、两角和与差的正、余弦公式、二倍角公式等相结合;第二问一般与三角形的面积、周长问题相结合,有时与基本不等式相结合求三角形的周长或面积的最值等.微专题1微专题2微专题1保 分 题1.已知函数f(x)=sin (ωx+)+2sin2()-1(ω>0)的相邻两对称轴间的距离为.(1)求f(x)的解析式;解析:由题意,函数f(x)=sin (ωx+)+2sin2[(ωx+)]-1=sin(ωx+)-cos (ωx+)=2sin (ωx+)=2sin ωx...
图片详情:
    篇5:高考数学复习专题三角函数与解三角形难点突破(含解析)高考数学复习专题三角函数与解三角形难点突破(含解析)资料可供全国地区适用。
大致详情:三角函数与解三角形 题型一 利用正、余弦定理解三角形例1 (12分)(2021·北京卷)已知在△ABC中,c=2bcos B,C=.(1)求B的大小;(2)在三个条件中选择一个作为已知,使△ABC存在且唯一确定,并求BC边上的中线的长度.①c=b;②周长为4+2;③面积为S△ABC=.第一步 利用正弦定理、余弦定理对条件式进行边角互化第二步 由三角方程或条件式求角第三步 利用条件式或正、余弦定理构建方程求边长第四步 检验易错易混、规范解题步骤得出结论训练1 (2021·株洲一模)在①sin B=cos B+1,②2bsin A=atan B,③(a-c)sin A+csin...
图片详情:
   篇6:2022-2023学年苏教版(2019)必修二第十一章 解三角形 单元测试卷(Word版含解析)2022-2023学年苏教版(2019)必修二第十一章 解三角形 单元测试卷(Word版含解析)资料可供全国地区适用。
大致详情:第十一章 解三角形 单元测试卷学校:___________姓名:___________班级:___________考号:___________一、选择题(共32分)1、(4分)已知的内角A,B,C所对的边分别为a,b,c,且,,,则边上的中线长为( )A.49 B.7 C. D.2、(4分)中,,则其最大内角的余弦值为( )A. B. C. D.3、(4分)已知A,B,C为的三个内角,且其对边分别为a,b,c,若,且,则( ).A. B. C. D.4、(4分)在中,角A,B,C的对边分别为a,b,c,若,则的值为( ).A. B. C. D.5、(4分)...
图片详情:
    篇7:【题型技巧解读】新高考数学 三角函数与解三角形 专题3-三角恒等变换与解三角形(原卷版+解析版)【题型技巧解读】新高考数学 三角函数与解三角形 专题3-三角恒等变换与解三角形(原卷版+解析版)资料可供全国地区适用。
大致详情:中小学教育资源及组卷应用平台小题考法专题三 三角恒等变换与解三角形一、保分小题落实练一、选择题例1.在平面直角坐标系中,角α的始边与x轴的正半轴重合,终边与单位圆交于点P,则sin=( )21·cn·jy·comA. B.-C. D.-例2.已知cos 2α+3cos α=1,则cos α=( )A. B.-C. D.-例3.已知sin=,且θ∈,则cos=( )A.0 B.C.1 D.例4.已知cos=2cos(π-α),则tan=( )A.-3 B.3C.- D.例5.已知f(x)=tan x+,则f的值为( )A...
图片详情:
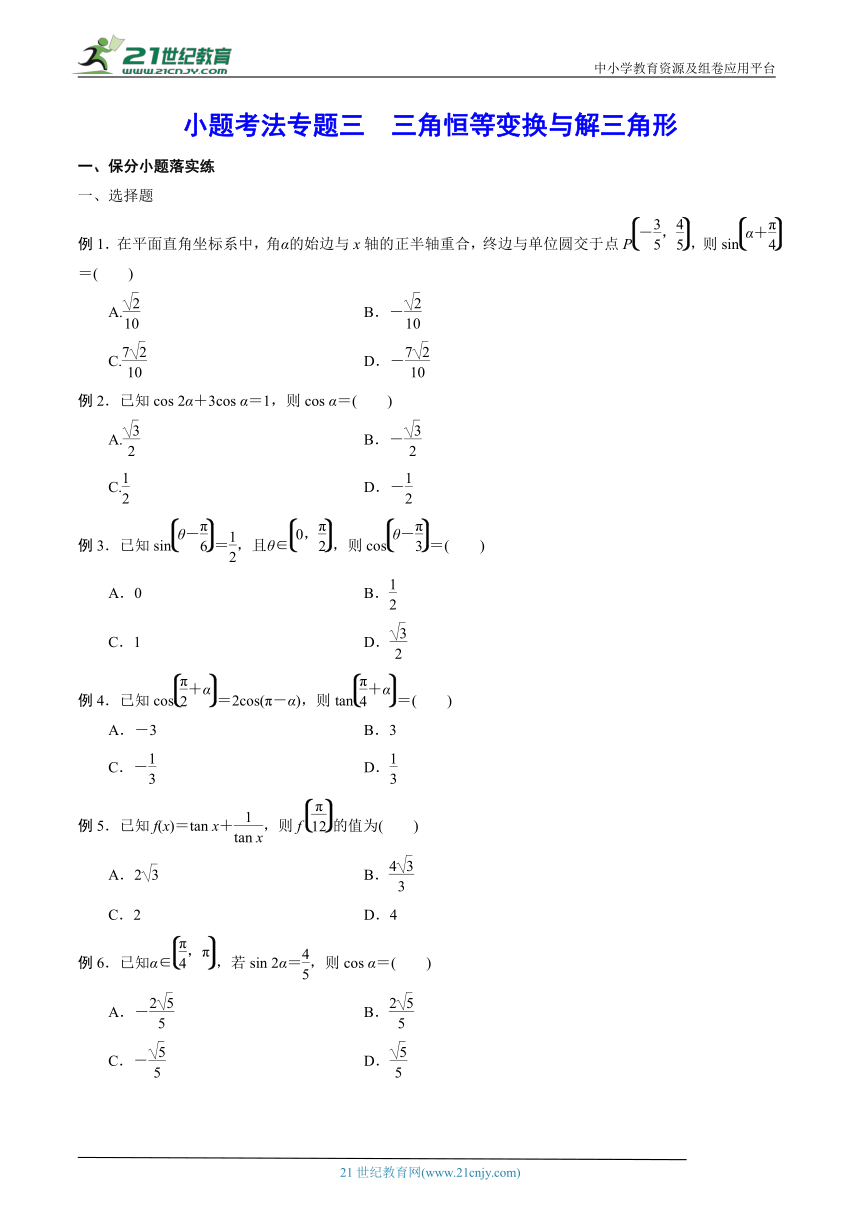  篇8:高中数学解三角形十大方法 素材高中数学解三角形十大方法 素材资料可供全国地区适用。
大致详情:解三角形中常用的方法姓名:1.正弦定理中边角互化的条件:次方必须相同,边看边,角看角。2.当遇到三个角时,必须化掉其中的一个,利用A+B+C=π,诱导公式。3.当遇到中线时,可以用向量的方法解决。4.大边对大角。5.求边的取值范围,往往都是转化成角的取值范围,利用三角函数解决。6.知道哪个角就用哪个角的公式。7.判断三角形解的个数,用余弦定理建立关于第三条边的一元二次方程,用△。8.当遇到比值或倍数时,可以设未知数x。9.已知sin cos tan 其中一个,画直角三角形求数值,符号根据象限确定。10.关于角平分线,利用角相等,条件可以反复利用。11.在大三角形中和小三...
图片详情:
 篇9:第11章 解三角形 正余弦定理在解三角形中的应用知识点总结与题型归纳 学案第11章 解三角形 正余弦定理在解三角形中的应用知识点总结与题型归纳 学案资料可供全国地区适用。
大致详情:11.3正弦余弦定理在三角形中的应用知识点(一). 正弦定理和余弦定理1.公式在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC的外接圆半径,则定理 正弦定理 余弦定理内容 ===2R. a2=b2+c2-2bccosA; b2=c2+a2-2cacosB; c2=a2+b2-2abcosC变形 (1)a=2Rsin A,b=2Rsin B,c=2Rsin C; (2)a∶b∶c=sin A∶sin B∶sin C; (3)==2R. ; ; .2.三角形常用面积公式:(1)S=a·ha(ha表示边a上的高);(2).3.常用结论:(1).在△ABC中,...
图片详情:
    篇10:2022-2023学年人教B版2019必修四第九章 解三角形 单元测试卷(word版含解析)2022-2023学年人教B版2019必修四第九章 解三角形 单元测试卷(word版含解析)资料可供全国地区适用。
大致详情:第九章 解三角形 单元测试卷学校:___________姓名:___________班级:___________考号:___________一、选择题(共40分)1、(4分)已知的内角A,B,C满足,面积S满足,记a,b,c分别为A,B,C所对的边,则下列不等式一定成立的是( )A. B. C. D.2、(4分)已知的内角A,B,C所对的边分别为a,b,c,且,,,则边上的中线长为( )A.49 B.7 C. D.3、(4分)中,,则其最大内角的余弦值为( )A. B. C. D.4、(4分)已知a,b,c分别为三个内角A,B,C的对边,,,若三角形有两解,则b的...
图片详情:
  篇11:第五章三角函数解三角形第八节解三角形的实际应用(课件+练习)北师大版适用于新教材2024版高考数学一轮总复习第五章三角函数解三角形第八节解三角形的实际应用(课件+练习)北师大版适用于新教材2024版高考数学一轮总复习资料可供全国地区适用。
大致详情:课时规范练25基础巩固组1.(2023·山西临汾高三月考)某地对该地某湖泊进行治理,在治理前,需测量该湖泊的相关数据.如图所示,测得∠A=23°,∠C=120°,AC=60米,则A,B间的直线距离约为(参考数据sin 37°≈0.6)( )A.60米 B.120米 C.150米 D.300米答案:C解析:由题设,∠B=180°-∠A-∠C=37°,在△ABC中,,即,所以AB=≈150米.故选C.2.如图为2022年北京冬奥会首钢滑雪大跳台示意图,为测量大跳台最高点P距地面的距离,小明同学在A点测得P的仰角为30°,∠ABO=120°,∠BAO=30°,AB=60(单位:m)(点...
图片详情:
    篇12:押题03 解三角形【含解析版】押题03 解三角形【含解析版】资料可供全国地区适用。
大致详情:中小学教育资源及组卷应用平台押题03 解三角形(2022·河北正定中学高三模拟)从①,②这两个条件中选一个,补充在下面问题中,并解答.已知的内角,,的对边分别为,,,且 .(1)求的值;(2)若的外接圆半径为,求的最大值.(注:如果选择多个条件分别作答,按第一个解答记分)【解析】(1)若选①:由,得,由余弦定理得:,又因为,所以 若选②:由,得即,故又因为,所以,所以,所以(2)由正弦定理得:,即,解得, 又由余弦定理得:,即所以,当且仅当“”时取等号. 所以的最大值为6.【押题理由】 由于新高考删除了解答题的选...
图片详情:
  篇13:学考复习之解三角形 练习(含解析)学考复习之解三角形 练习(含解析)资料可供全国地区适用。
大致详情:中小学教育资源及组卷应用平台学考复习之解三角形1.在中,角A,B,C的对边分别为a,b,c,,(1)求C的大小;(2)已知,求b的值.【答案】(1)(2)2【解析】(1),∴,.(2),,∴2.在中,角A,B,C所对的边分别为a,b,c,且,.(1)若,求B;(2)若,求b.【答案】(1)(2)或【解析】(1)由余弦定理,得,又,∴.(2)由正弦定理,得,∵,∴或.当时,,∴;当时,,∴.综上,或.3.如图,在平面四边形中,,,,.(1)求的值;(2)若,求△的边上高的大小.【答案】(1)(2)【解析】(1)在中,由正弦定理得 ,即...
图片详情:
   篇14:新教材适用2024版高考数学一轮总复习第4章三角函数解三角形第6讲解三角形课件(课件共81张PPT+作业)新教材适用2024版高考数学一轮总复习第4章三角函数解三角形第6讲解三角形课件(课件共81张PPT+作业)资料可供全国地区适用。
大致详情:练案[28] 第六讲 解三角形A组基础巩固一、选择题1.(2023·云南省宾川高三上学期数学摸底试卷)在△ABC中,已知(a+b+c)(b+c-a)=3bc,则角A等于( )A.30° B.60°C.120° D.150°2.在△ABC中,c=,A=75°,B=45°,则△ABC的外接圆的面积为( )A. B.πC.2π D.4π3.(2023·安徽合肥模拟)在△ABC中,A=60°,AB=2,且△ABC的面积为,则BC的长为( )A. B.C.2 D.24.在△ABC中,若=,则△ABC的形状是( )A.等腰三角形B.直角三角形C.等腰直角三...
图片详情:
   篇15:解三角形中求周长、面积及其范围问题 讲义(含答案)解三角形中求周长、面积及其范围问题 讲义(含答案)资料可供全国地区适用。
大致详情:解三角形(2)【公式】正弦定理:变形:余弦定理:变形:三角关系:在三角形中,三角形面积公式:辅助角公式:基本不等式:和(差)角公式:二倍角公式:平方关系: 商数关系:【求面积】1.在中,已知,其中为的面积,,,分别为角,,的对边.(1)求角的值;(2)若,求的值.2.在中,角A,B,C所对的边分别为a,b,c,且.(1)求角A;(2)若,,求的面积.3.在中,内角A,B,C的对边分别为a,b,c,已知.(1)求角C的值;(2)若,当边c取最小值时,求的面积.4.在中,,,分别是角,,的对边,且.(...
图片详情:
    Tags:三角形,单元,测试,精选,15篇

|
21世纪教育网,教育资讯交流平台




